
들어가며
본 포스팅은 <파이썬 알고리즘 인터뷰> 책에서 다룬 리트코드 문제들을 다루고 있습니다.
문제들은 모두 리트코드에서 출제된 문제들이며, 문제 풀이의 많은 부분을 책의 힌트와 해설을 참고하였습니다.
포스팅되는 모든 문제들의 목록과 풀이는 파이썬 알고리즘 인터뷰에서 제공하는 깃허브에서 확인하실 수 있습니다.
문제
Given the array of integers nums, you will choose two different indices i and j of that array. Return the maximum value of (nums[i]-1)*(nums[j]-1).
배열에서 (nums[i]-1)*(nums[j]-1)가 가장 큰 값을 출력하라
입출력 예시
Example 1:
Input: nums = [3,4,5,2]
Output: 12
Explanation: If you choose the indices i=1 and j=2 (indexed from 0), you will get the maximum value, that is, (nums[1]-1)*(nums[2]-1) = (4-1)*(5-1) = 3*4 = 12.
Example 2:
Input: nums = [1,5,4,5]
Output: 16
Explanation: Choosing the indices i=1 and j=3 (indexed from 0), you will get the maximum value of (5-1)*(5-1) = 16.
Example 3:
Input: nums = [3,7]
Output: 12
생각과정
(nums[i]-1)*(nums[j]-1)가 가장 큰 값은 결국 배열에서 가장 큰 요소 두개를 골라서 주어진 식에 집어 넣으면 된다.
이 문제를 풀면서 파이썬 docs에 최소 힙을 최대 힙으로 바꾸는 방법을 새롭게 알게 되었는데 아래와 같다.
import heapq
nums = [4, 1, 7, 3, 8, 5]
heap = []
for num in nums:
heapq.heappush(heap, (-num, num)) # (우선 순위, 값)
while heap:
print(heapq.heappop(heap)[1]) # index 1
튜플을 이용한 방법인데, 튜블의 0번째에는 음수로 된 num, 뒤에는 num을 넣어주면 힙의 가장 작은 값이 위로 오는 특성으로 인해 최소 힙이 최대 힙이 될 수 있다. 위의 코드를 실행시켜보면 아래와 같이 출력된다.
8
7
5
4
3
1
이 방식을 이용해서 문제를 풀어보자!
풀이
def maxProduct(nums):
if len(nums) == 2:
return (nums[0] - 1) * (nums[1] - 1)
heap = []
# 최대 힙으로 바꾸는 로직 (튜플을 이용)
for num in nums:
heapq.heappush(heap, (-num, num))
# 인덱스 기준으로 정렬
heap.sort()
# 뽑아보려고 한거
i = heapq.heappop(heap)
j = heapq.heappop(heap)
return (i[1] - 1) * (j[1] - 1)
여기서 봐야할 부분은 최대 힙으로 바꾸는 로직과 sort()를 하는 부분이다.
위에서 최소 힙을 최대 힙으로 바꾸는 방법대로 nums를 돌리면 heap은 다음과 같이 정렬된다.
[(-5, 5), (-3, 3), (-4, 4), (-2, 2)]
이걸 그림으로 나타내면 다음과 같다
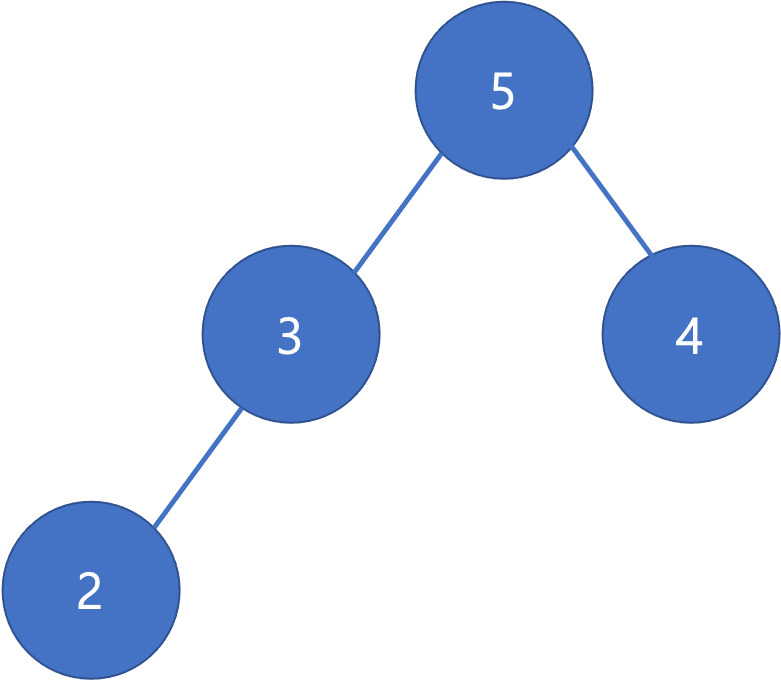
튜플을 이용해 최소 힙을 최대 힙으로 바꿀 수 있는 이유는 우선순위로 정한 튜플의 인덱스 0번째 요소 덕분이다.
힙은 기본적으로 최소 값을 위로 올리는 특성을 가졌는데, 0번째 요소를 음수로 해주면 숫자가 클 수록 작은 값이 된다.
그러므로 힙에 집어넣었을 때, 0번째 인덱스 기준으로 힙이 정렬되고 1번째 인덱스에 원하는 최대 힙의 결과값을 얻을 수 있게 되는 것이다.
최소 힙을 최대 힙으로 바꿔주었다면 최댓값을 뽑기 위해 sort() 함수로 정렬을 해주고, 원하는 값을 뽑아주면 해결!
마치며
그 어느 자료구조보다 쉬운 힙이었다. 개념 정리는 오래 걸렸지만 이렇게 내가 생각한게 코드로 구현되니 기분이 꽤나 좋다.
알고리즘 초보 오늘도 1스택 쌓았다!
'Algorithm > Leetcode' 카테고리의 다른 글
| [leetcode] 108. 정렬된 배열의 이진 탐색 트리 변환 (Convert Sorted Array to Binary Search Tree) (0) | 2022.05.24 |
|---|---|
| [leetcode] 226. 이진 트리 반전 (Invert Binary Tree) (0) | 2022.05.24 |
| [leetcode] 104. 이진 트리의 최대 깊이 (Maximum Depth of Binary Tree) (0) | 2022.05.24 |
| [leetcode] 51. N-Queen (0) | 2022.05.22 |
| [leetcode] 200. 섬의 개수 (Number of Islands) (0) | 2022.05.20 |
