
들어가며
본 포스팅은 <파이썬 알고리즘 인터뷰> 책에서 다룬 리트코드 문제들을 다루고 있습니다.
문제들은 모두 리트코드에서 출제된 문제들이며, 문제 풀이의 많은 부분을 책의 힌트와 해설을 참고하였습니다.
포스팅되는 모든 문제들의 목록과 풀이는 파이썬 알고리즘 인터뷰에서 제공하는 깃허브에서 확인하실 수 있습니다.
문제
Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.
A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.
오름차순으로 정ㄹ려된 배열을 높이 균형 이진 탐색 트리로 변환하라.
높이 균형 트리란 모든 노드의 두 서브트리 간 깊이 차이가 1 이하인 것을 말한다.
입출력 예시
Example 1:

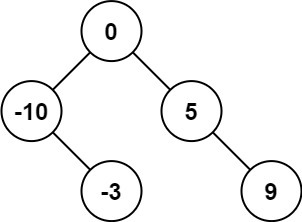
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:
Example 2:
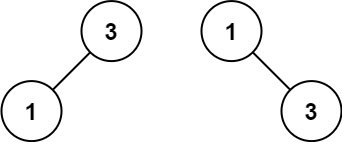
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.
풀이
앞서 이진 탐색 트리 TIL에서 정리한 것처럼 배열을 이진 탐색 트리로 만들 때는 정렬된 배열을 사용해야한다. 배열을 절반씩 쪼개는 이진 검색을 사용해서 이진 탐색 트리를 만들 수 있기 때문이다.
아래는 이해하기 쉽게 주어진 배열에 -7과 7을 집어넣어서 완전 이진 탐색 트리로 만든 그림이다.
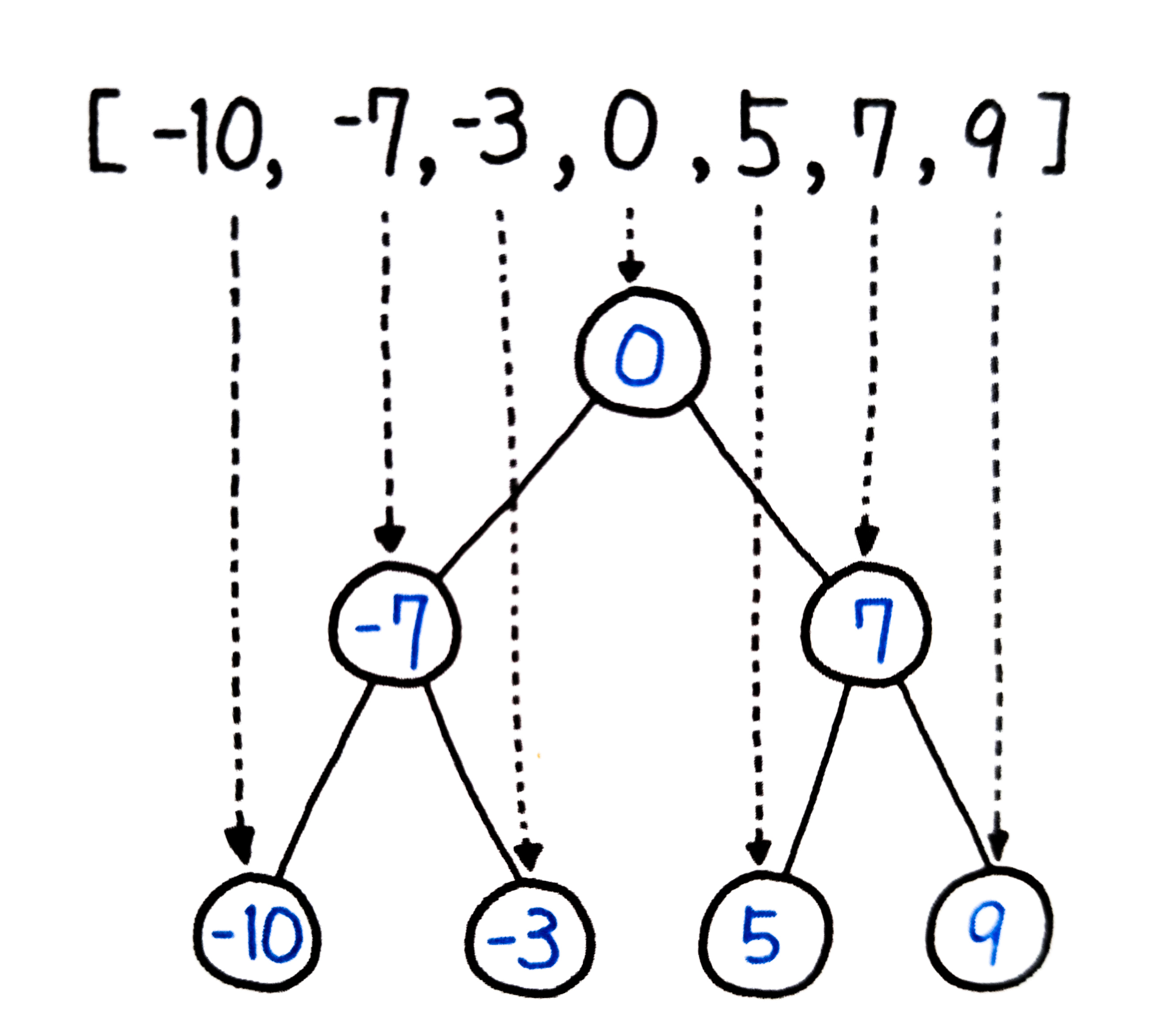
위 그림을 이진 검색으로 생각해보자면,
우선 주어진 배열인 [-10, -7, -3, 0, 5, 7, 9]를 절반으로 쪼개보자. 가운데 값인 0을 기준으로 [-10, -7, -3] [0] [5, 7, 9]로 나눠질 수 있다. 이걸 다시 반으로 쪼개면 그림과 같은 모양이 나타난다. 이게 이진 검색의 마법이다! 신기하다
문제 풀이 흐름을 이해했으니 전체 코드와 함께 코드의 흐름도 함께 이해해보자
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def sortedArrayToBST(nums):
if not nums:
return None
# 주어진 배열을 반으로 쪼개준다. // 연산자는 나눈 몫의 정수만 남겨준다.
mid = len(nums) // 2
node = TreeNode(nums[mid])
node.left = sortedArrayToBST(nums[:mid])
node.right = sortedArrayToBST(nums[mid + 1:])
return node
TreeNode 클래스는 이진 탐색 트리를 위한 클래스이므로 항상 따라다니기도 하고, 리트코드에서는 기본으로 선언이 되어있으니 리트코드에는 따로 입력할 필요는 없다
우리는 원래 목적인 sortedArrayToBST 함수를 살펴보자
첫번째 조건문은 nums가 비어있을 때를 대비한 예외처리이다. 예외처리는 항상 잊지 말고 넣어주자.
그 다음 mid가 이진 검색을 위한 이번 문제의 포인트인데, 주어진 배열을 반으로 쪼개서 인덱스로 만들어주는 간단한 코드이다.
첫번째로 주어진 예시를 가지고 생각해보면, [-10,-3,0,5,9]의 길이인 5를 절반으로 쪼개면 2 ( // 연산자로 소수점자리는 버린다) 가 나온다. 이 mid를 인덱스로 가지고 있는 값이 부모 노드가 된다. 그럼 왼쪽과 오른쪽 노드는 반으로 쪼개고 남은 나머지 왼쪽 배열과 오른쪽 배열이 될 것이다.
파이썬의 슬라이싱 문법에서 [a:b]의 b는 원하는 범위의 -1까지 리턴해주므로 왼쪽 노드에 들어갈 배열은 처음부터 mid까지의 범위가 되고, 당연히 오른쪽 노드는 mid 인덱스의 다음 인덱스인 mid + 1부터 마지막 인덱스가 된다.
여기서의 재귀는 크게 어렵지 않다. 처음 부모 노드를 정하고, 왼쪽과 오른쪽 자식 노드를 정한 것과 똑같은 과정을 반복해주면 된다.
이렇게 간단하게 정렬된 배열을 이진 탐색 트리로 만들기 해결!
마치며
이진 탐색의 로그 마법! 알고리즘 제대로 구현만 할 줄 알게 된다면 재밌을 것 같다.
'Algorithm > Leetcode' 카테고리의 다른 글
| [leetcode] 1464. 배열에 있는 두 요소의 최대 곱 (Maximum Product of Two Elements in an Array) (0) | 2022.05.26 |
|---|---|
| [leetcode] 226. 이진 트리 반전 (Invert Binary Tree) (0) | 2022.05.24 |
| [leetcode] 104. 이진 트리의 최대 깊이 (Maximum Depth of Binary Tree) (0) | 2022.05.24 |
| [leetcode] 51. N-Queen (0) | 2022.05.22 |
| [leetcode] 200. 섬의 개수 (Number of Islands) (0) | 2022.05.20 |