
들어가며
본 포스팅은 <파이썬 알고리즘 인터뷰> 책에서 다룬 리트코드 문제들을 다루고 있습니다.
문제들은 모두 리트코드에서 출제된 문제들이며, 문제 풀이의 많은 부분을 책의 힌트와 해설을 참고하였습니다.
포스팅되는 모든 문제들의 목록과 풀이는 파이썬 알고리즘 인터뷰에서 제공하는 깃허브에서 확인하실 수 있습니다.
문제
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
두 개의 퀸이 서로 공격하지 않도록 n x n 체스판에 n개의 퀸을 배치하라.
N*N 체스판에 N개의 퀸을 배치할 수 있는 경우의 수를 센다.
- 퀸은 상하좌우, 대각선 방향으로 거리 제한 없이 이동할 수 있다.
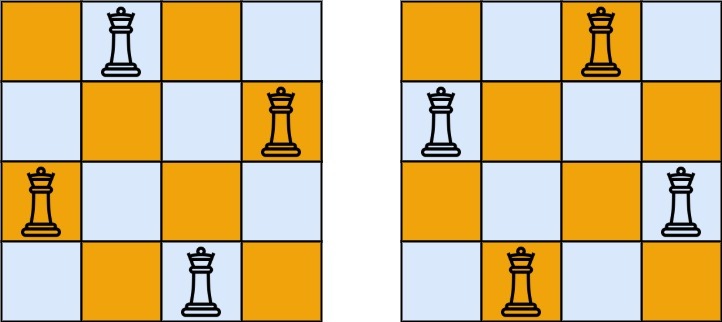
입출력 예시
Example 1:
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]Example 2:
Input: n = 1
Output: [["Q"]]문제 정리
첫 번째 줄에 (0,0), (0,1) (0,2), (0,3)에 퀸을 두고 그 다음에 (1, 0), (0,2) (0,3), (0,4)을 놓아보고 하는 모든 경우의 수 탐색문제이다.
따라서 DFS를 사용하는게 적절한데, 문제는 N * N 행과 열의 모든 경우의 수를 탐색하면 시간이 어마무시하게 소요된다.
N이 4일 때의 경우의 수는 그래도 큰 종이가 있다면 손으로 그려볼 수도 있는 크기지만 N이 커지면 커질 수록 경우의 수가 기하급수적으로 커지게 된다. N이 8만 되어도 178,462,987,637,760가지의 경우의 수가 있다고 하니, 이 경우의 수를 모두 탐색하는 건 말이 안된다.
이럴 때 이용할 수 있는게 바로 백트래킹(Bcaktracking)이다.
BFS가 최단 경로나 최소 횟수 문제에 적합하다고 했으니 BFS로 풀면 금방 해결되는거 아냐? 라는 의문이 들었지만, BFS는 노드가 많아질 수록 탐색해야할 노드가 많아지기 때문에 시간초과나 메모리초과가 날 가능성이 있어 DFS로 접근하는게 더 쉽고 간단하게 풀린다고 한다.
추가적으로 백트래킹의 대부분 문제들이 파이썬으로 풀기에 부적합하다고 한다. 파이썬이 다른 언어들에 비해 수행속도가 느리기 때문이다.
하지만 지금은 공부가 주목적이기 때문에 계속 사용해오던 파이썬으로 문제를 분석하고 공부해보기로 하자.
풀이
*해당 풀이는 항해99 강의에서 제공한 코드로 리트코드에서 요구하는 문자열 출력값이 아닌 1차원배열 숫자로 출력되므로 일련의 처리과정을 거쳐야한다. 하지만 나는 코드를 이해하는 것이 목적이므로 해당 처리는 넘어가도록 한다.
def n_queen(n):
visited = [-1] * n
answers = []
# 1) dfs구현
def dfs(row):
# 모든 경우의 수를 찾았을 때, answers에 결과값을 담고 리턴
if row >= n:
answers.append(visited)
print(visited)
return
# visited[row]의 값을 결정한다 -> 퀸을 둔다.
# 가능한 열의 범위는 0 ~ n - 1이다. 인덱스 번호는 0부터 시작하기 때문이다.
# 열의 개수 만큼 반복 한다. 그 행의 열을 돌면서 어디다 퀸을 둘 지 판단해야하기 때문
for col in range(n):
visited[row] = col
# 첫번째 줄에 퀸을 두었으면, 다음 줄에 퀸을 두러간다.
# is_ok_on(row) -> 조건으로 주어진, 퀸이 다음 퀸을 잡지 못하는 위치를 판별하는 함수.
if is_ok_on(row):
# 첫번째 줄의 판별이 끝났다면 다음 줄에 퀸을 놓으러 간다.. ex) (0, 0) -> (1, 0)
dfs(row + 1)
# 퀸이 다른 퀸을 잡을 수 있는 지 판별하는 함수
def is_ok_on(nth_row):
for row in range(nth_row):
# 퀸이 같은 세로줄에 있다면, 혹은 대각선에 있다면, False를 리턴
# 대각선은 현재 놓여진 퀸과 새로 놓으려는 퀸의 행 간의 차이 == 열 간의 차이일 때, 판단가능 -> 그림으로 설명하기
if visited[nth_row] == visited[row] or nth_row - row == abs(visited[nth_row] - visited[row]):
return False
# 세로줄과 대각선에 퀸이 놓여있지 않다면 다음 퀸을 놓으러 갈 수 있도록 True 리턴
return True
# 0번째 행에 퀸을 둔다.
dfs(0)
# 결과 리턴
return answers
재귀함수 + DFS는 정말 이해하기가 너무 어렵다. 그러니 그림으로 천천히 코드를 분해해가며 이해해보자.
코드가 실행되는 순서에 따라 일일히 쪼개놨으므로 헷갈린다면 전체코드와 함께 보도록 하자! 나는 일일히 뜯어보는게 이해하기 편해서 하나하나 분해시키면서 풀이를 따라가기로 했다.
dfs(0)
def dfs(row):
for col in range(n):
visited[row] = col
if is_ok_on(row):
dfs(row + 1)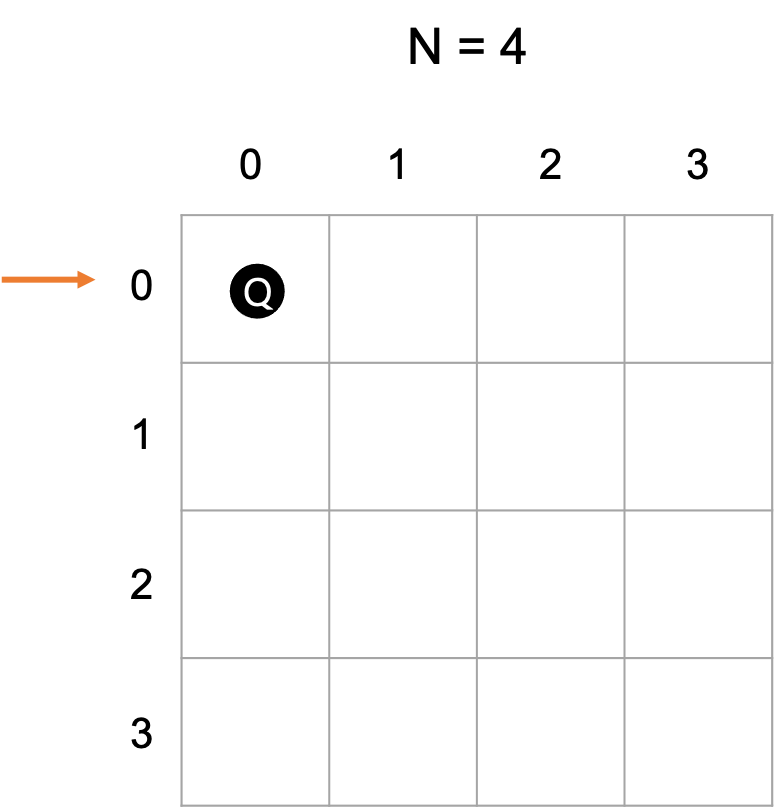
가장 먼저 (0, 0) 위치에 퀸을 둔다. 첫번째 경우의 수이다. 바로 윗 줄에 나오는 for문을 n번 돌림으로써 최종적으로 1행의 4개열을 모두 돌게 된다.
퀸을 두었다면 이 퀸을 잡을 수 있는 다른 퀸이 있는 지 판별하는 is_ok_on(nth_row)로 넘어가게 되지만 이후에 놓인 퀸들이 없으므로 True를 반환하고 재귀 호출을 한다.
이제 (1, 0)부터 퀸을 둘 수 있는 지 판별하기 위해 재귀 호출 함수로 들어온다. 역시 똑같이 (1, 0) 위치에 퀸을 두고 해당 퀸을 잡을 수 있는 퀸이 있는 지 판별하러 간다.
def is_ok_on(nth_row):
for row in range(nth_row):
# 퀸이 같은 세로줄에 있다면, 혹은 대각선에 있다면, False를 리턴
# 대각선은 현재 놓여진 퀸과 새로 놓으려는 퀸의 행 간의 차이 == 열 간의 차이일 때, 판단가능
if visited[nth_row] == visited[row] or nth_row - row == abs(visited[nth_row] - visited[row]):
return False
# 세로줄과 대각선에 퀸이 놓여있지 않다면 다음 퀸을 놓으러 갈 수 있도록 True 리턴
return True
우선 for문으로 0번째 행부터 nth_row - 1번째 행을 꺼내온다. 이전 행(위쪽 줄)에 퀸이 놓여있는지 판별하기 위함이다.
같은 열에 있는 지 판별하는 조건문은 어렵지 않다. 현재 퀸의 열과 이전 퀸의 열이 같은 지만 판별하면 된다.
대각선이 한번에 판단되지 않았는데, 아래 그림처럼 생각하면 어렵지 않다.
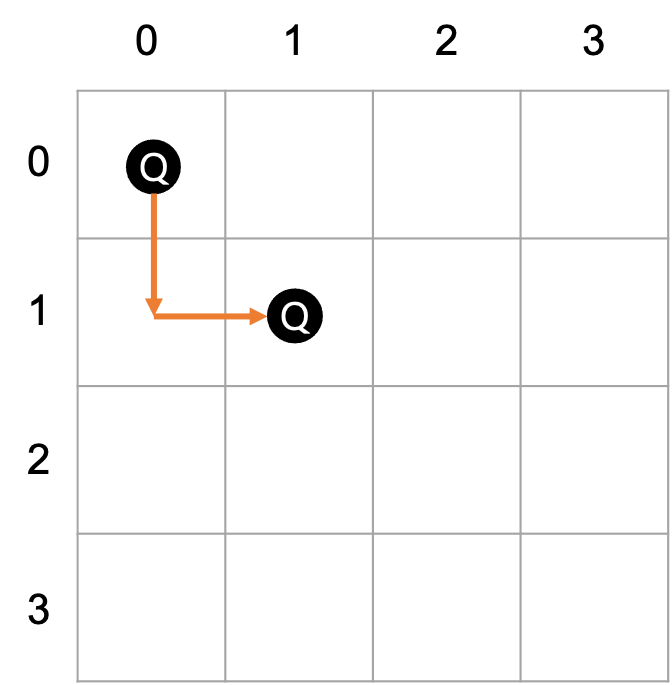
현재 퀸보다 좌측에 있는 퀸의 대각선 위치는 nth_row - row 즉, 행 간의 차이와 visited[nth_row] - visited[row] 즉, 열 간의 차이가 같은 위치이다.
예를들어, 그림에서 현재 퀸은 (1, 1)에 있고 가장 첫번째 놓인 퀸은 (0, 0)에 있다. 행 간의 차이와 열 간의 차이는 1과 1이므로 대각선에 위치해있다. 만약 0번째 행의 퀸이 1번째 행의 퀸보다 오른쪽에 놓이게 되면 열 간의 차이가 음수가 나오게 되는데 결국 대각선 위치에 있는건 똑같기 때문에 abs()를 이용하여 절대값으로 만들어줘 비교한다.
1번째 행에서 조건에 중족하는 퀸의 위치를 찾게되면 다음 그림과 같다
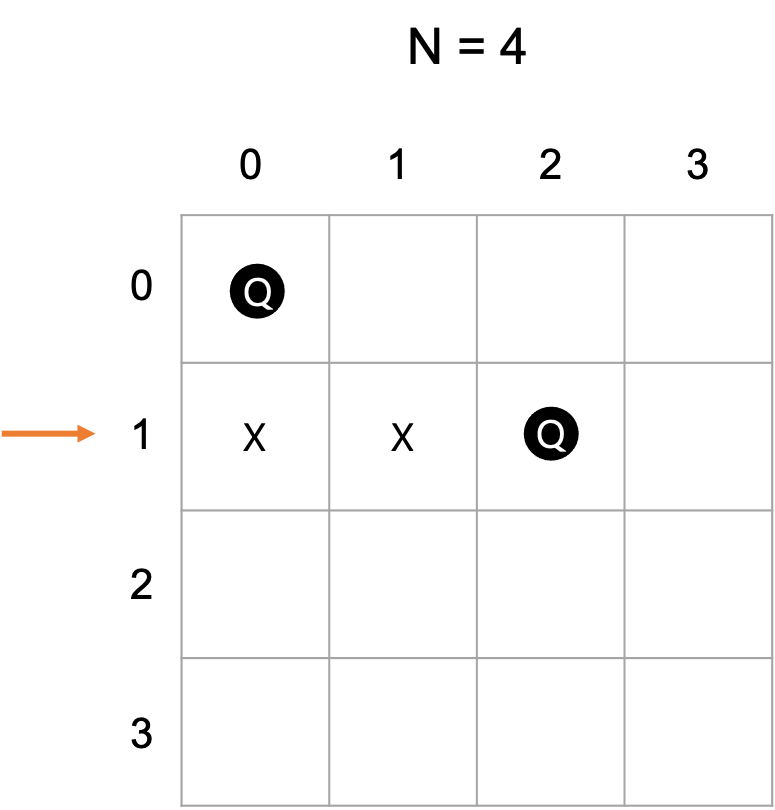
같은 방식으로 계속 재귀 함수를 타고 들어가다보면 마지막 행에서 가능한 경우의 수가 없는 상황이 생긴다.
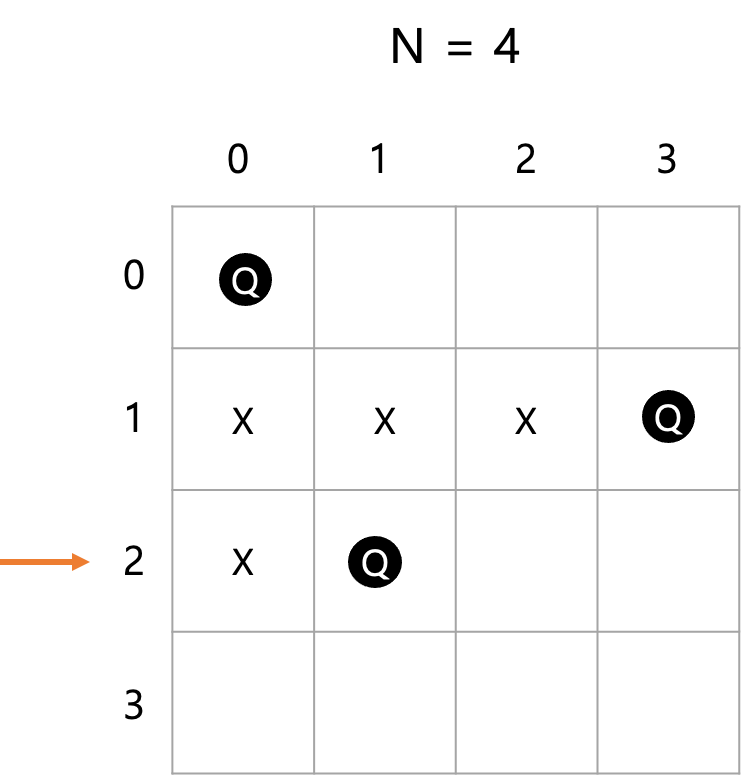
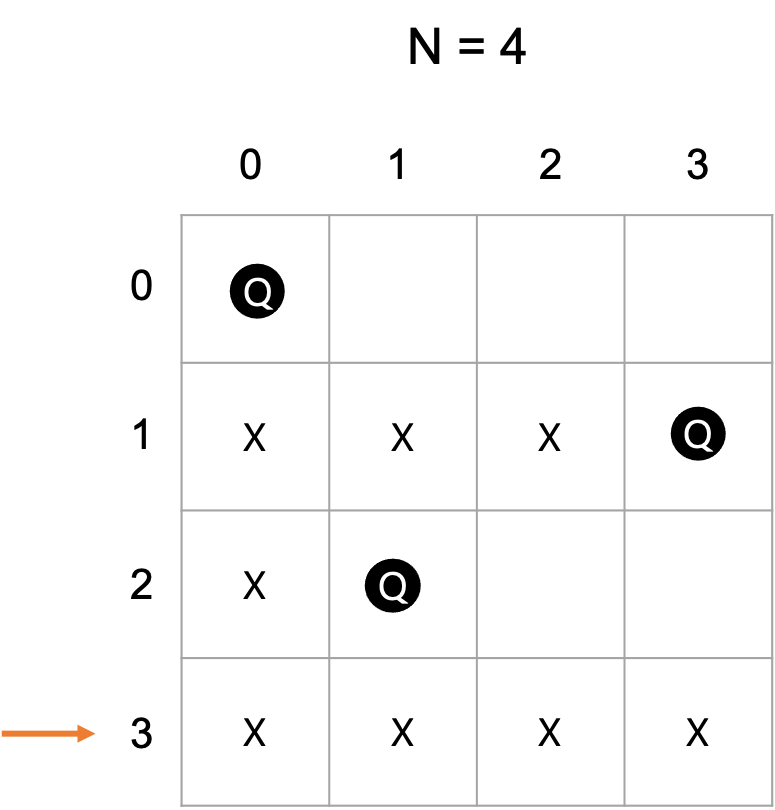
이렇게 되면 4번째 행의 모든 판단문이 False로 나오게 되고 재귀를 탈출한다.
그 이후는 쭉 같은 과정을 반복하다가 결국 조건에 만족하는 경우의 수를 발견하게 되면 answer에 넣어주고 다른 경우의 수를 탐색하기 위해 위의 과정을 다시 반복한다.
마치며
이해하는 데에만 한참 걸린 문제이다. 내가 풀 수 있을 지는 잘 모르겠다....
'Algorithm > Leetcode' 카테고리의 다른 글
| [leetcode] 226. 이진 트리 반전 (Invert Binary Tree) (0) | 2022.05.24 |
|---|---|
| [leetcode] 104. 이진 트리의 최대 깊이 (Maximum Depth of Binary Tree) (0) | 2022.05.24 |
| [leetcode] 200. 섬의 개수 (Number of Islands) (0) | 2022.05.20 |
| [leetcode] 706. 해시맵 디자인 (Design HashMap) (0) | 2022.05.19 |
| [leetcode] 3. 중복 문자 없는 가장 긴 부분 문자열 (Longest Substring WIthout Repeating Characters) (0) | 2022.05.18 |

들어가며
본 포스팅은 <파이썬 알고리즘 인터뷰> 책에서 다룬 리트코드 문제들을 다루고 있습니다.
문제들은 모두 리트코드에서 출제된 문제들이며, 문제 풀이의 많은 부분을 책의 힌트와 해설을 참고하였습니다.
포스팅되는 모든 문제들의 목록과 풀이는 파이썬 알고리즘 인터뷰에서 제공하는 깃허브에서 확인하실 수 있습니다.
문제
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
두 개의 퀸이 서로 공격하지 않도록 n x n 체스판에 n개의 퀸을 배치하라.
N*N 체스판에 N개의 퀸을 배치할 수 있는 경우의 수를 센다.
- 퀸은 상하좌우, 대각선 방향으로 거리 제한 없이 이동할 수 있다.

입출력 예시
Example 1:
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]Example 2:
Input: n = 1
Output: [["Q"]]문제 정리
첫 번째 줄에 (0,0), (0,1) (0,2), (0,3)에 퀸을 두고 그 다음에 (1, 0), (0,2) (0,3), (0,4)을 놓아보고 하는 모든 경우의 수 탐색문제이다.
따라서 DFS를 사용하는게 적절한데, 문제는 N * N 행과 열의 모든 경우의 수를 탐색하면 시간이 어마무시하게 소요된다.
N이 4일 때의 경우의 수는 그래도 큰 종이가 있다면 손으로 그려볼 수도 있는 크기지만 N이 커지면 커질 수록 경우의 수가 기하급수적으로 커지게 된다. N이 8만 되어도 178,462,987,637,760가지의 경우의 수가 있다고 하니, 이 경우의 수를 모두 탐색하는 건 말이 안된다.
이럴 때 이용할 수 있는게 바로 백트래킹(Bcaktracking)이다.
BFS가 최단 경로나 최소 횟수 문제에 적합하다고 했으니 BFS로 풀면 금방 해결되는거 아냐? 라는 의문이 들었지만, BFS는 노드가 많아질 수록 탐색해야할 노드가 많아지기 때문에 시간초과나 메모리초과가 날 가능성이 있어 DFS로 접근하는게 더 쉽고 간단하게 풀린다고 한다.
추가적으로 백트래킹의 대부분 문제들이 파이썬으로 풀기에 부적합하다고 한다. 파이썬이 다른 언어들에 비해 수행속도가 느리기 때문이다.
하지만 지금은 공부가 주목적이기 때문에 계속 사용해오던 파이썬으로 문제를 분석하고 공부해보기로 하자.
풀이
*해당 풀이는 항해99 강의에서 제공한 코드로 리트코드에서 요구하는 문자열 출력값이 아닌 1차원배열 숫자로 출력되므로 일련의 처리과정을 거쳐야한다. 하지만 나는 코드를 이해하는 것이 목적이므로 해당 처리는 넘어가도록 한다.
def n_queen(n):
visited = [-1] * n
answers = []
# 1) dfs구현
def dfs(row):
# 모든 경우의 수를 찾았을 때, answers에 결과값을 담고 리턴
if row >= n:
answers.append(visited)
print(visited)
return
# visited[row]의 값을 결정한다 -> 퀸을 둔다.
# 가능한 열의 범위는 0 ~ n - 1이다. 인덱스 번호는 0부터 시작하기 때문이다.
# 열의 개수 만큼 반복 한다. 그 행의 열을 돌면서 어디다 퀸을 둘 지 판단해야하기 때문
for col in range(n):
visited[row] = col
# 첫번째 줄에 퀸을 두었으면, 다음 줄에 퀸을 두러간다.
# is_ok_on(row) -> 조건으로 주어진, 퀸이 다음 퀸을 잡지 못하는 위치를 판별하는 함수.
if is_ok_on(row):
# 첫번째 줄의 판별이 끝났다면 다음 줄에 퀸을 놓으러 간다.. ex) (0, 0) -> (1, 0)
dfs(row + 1)
# 퀸이 다른 퀸을 잡을 수 있는 지 판별하는 함수
def is_ok_on(nth_row):
for row in range(nth_row):
# 퀸이 같은 세로줄에 있다면, 혹은 대각선에 있다면, False를 리턴
# 대각선은 현재 놓여진 퀸과 새로 놓으려는 퀸의 행 간의 차이 == 열 간의 차이일 때, 판단가능 -> 그림으로 설명하기
if visited[nth_row] == visited[row] or nth_row - row == abs(visited[nth_row] - visited[row]):
return False
# 세로줄과 대각선에 퀸이 놓여있지 않다면 다음 퀸을 놓으러 갈 수 있도록 True 리턴
return True
# 0번째 행에 퀸을 둔다.
dfs(0)
# 결과 리턴
return answers
재귀함수 + DFS는 정말 이해하기가 너무 어렵다. 그러니 그림으로 천천히 코드를 분해해가며 이해해보자.
코드가 실행되는 순서에 따라 일일히 쪼개놨으므로 헷갈린다면 전체코드와 함께 보도록 하자! 나는 일일히 뜯어보는게 이해하기 편해서 하나하나 분해시키면서 풀이를 따라가기로 했다.
dfs(0)
def dfs(row):
for col in range(n):
visited[row] = col
if is_ok_on(row):
dfs(row + 1)
가장 먼저 (0, 0) 위치에 퀸을 둔다. 첫번째 경우의 수이다. 바로 윗 줄에 나오는 for문을 n번 돌림으로써 최종적으로 1행의 4개열을 모두 돌게 된다.
퀸을 두었다면 이 퀸을 잡을 수 있는 다른 퀸이 있는 지 판별하는 is_ok_on(nth_row)로 넘어가게 되지만 이후에 놓인 퀸들이 없으므로 True를 반환하고 재귀 호출을 한다.
이제 (1, 0)부터 퀸을 둘 수 있는 지 판별하기 위해 재귀 호출 함수로 들어온다. 역시 똑같이 (1, 0) 위치에 퀸을 두고 해당 퀸을 잡을 수 있는 퀸이 있는 지 판별하러 간다.
def is_ok_on(nth_row):
for row in range(nth_row):
# 퀸이 같은 세로줄에 있다면, 혹은 대각선에 있다면, False를 리턴
# 대각선은 현재 놓여진 퀸과 새로 놓으려는 퀸의 행 간의 차이 == 열 간의 차이일 때, 판단가능
if visited[nth_row] == visited[row] or nth_row - row == abs(visited[nth_row] - visited[row]):
return False
# 세로줄과 대각선에 퀸이 놓여있지 않다면 다음 퀸을 놓으러 갈 수 있도록 True 리턴
return True
우선 for문으로 0번째 행부터 nth_row - 1번째 행을 꺼내온다. 이전 행(위쪽 줄)에 퀸이 놓여있는지 판별하기 위함이다.
같은 열에 있는 지 판별하는 조건문은 어렵지 않다. 현재 퀸의 열과 이전 퀸의 열이 같은 지만 판별하면 된다.
대각선이 한번에 판단되지 않았는데, 아래 그림처럼 생각하면 어렵지 않다.

현재 퀸보다 좌측에 있는 퀸의 대각선 위치는 nth_row - row 즉, 행 간의 차이와 visited[nth_row] - visited[row] 즉, 열 간의 차이가 같은 위치이다.
예를들어, 그림에서 현재 퀸은 (1, 1)에 있고 가장 첫번째 놓인 퀸은 (0, 0)에 있다. 행 간의 차이와 열 간의 차이는 1과 1이므로 대각선에 위치해있다. 만약 0번째 행의 퀸이 1번째 행의 퀸보다 오른쪽에 놓이게 되면 열 간의 차이가 음수가 나오게 되는데 결국 대각선 위치에 있는건 똑같기 때문에 abs()를 이용하여 절대값으로 만들어줘 비교한다.
1번째 행에서 조건에 중족하는 퀸의 위치를 찾게되면 다음 그림과 같다

같은 방식으로 계속 재귀 함수를 타고 들어가다보면 마지막 행에서 가능한 경우의 수가 없는 상황이 생긴다.


이렇게 되면 4번째 행의 모든 판단문이 False로 나오게 되고 재귀를 탈출한다.
그 이후는 쭉 같은 과정을 반복하다가 결국 조건에 만족하는 경우의 수를 발견하게 되면 answer에 넣어주고 다른 경우의 수를 탐색하기 위해 위의 과정을 다시 반복한다.
마치며
이해하는 데에만 한참 걸린 문제이다. 내가 풀 수 있을 지는 잘 모르겠다....
'Algorithm > Leetcode' 카테고리의 다른 글
| [leetcode] 226. 이진 트리 반전 (Invert Binary Tree) (0) | 2022.05.24 |
|---|---|
| [leetcode] 104. 이진 트리의 최대 깊이 (Maximum Depth of Binary Tree) (0) | 2022.05.24 |
| [leetcode] 200. 섬의 개수 (Number of Islands) (0) | 2022.05.20 |
| [leetcode] 706. 해시맵 디자인 (Design HashMap) (0) | 2022.05.19 |
| [leetcode] 3. 중복 문자 없는 가장 긴 부분 문자열 (Longest Substring WIthout Repeating Characters) (0) | 2022.05.18 |
