
들어가며
나에게 맞는 알고리즘 공부 방법을 찾고나니 한결 마음이 가벼워졌다. 또, 오늘은 문제가 쉬웠는지 직접 문제 풀이에 성공해서 꽤나 뿌듯했다.
이 기쁜 마음을 안고, 오늘의 TIL은 힙의 개념과 문제풀이, 새로 알게 된 개념을 정리해보고자 한다.
힙
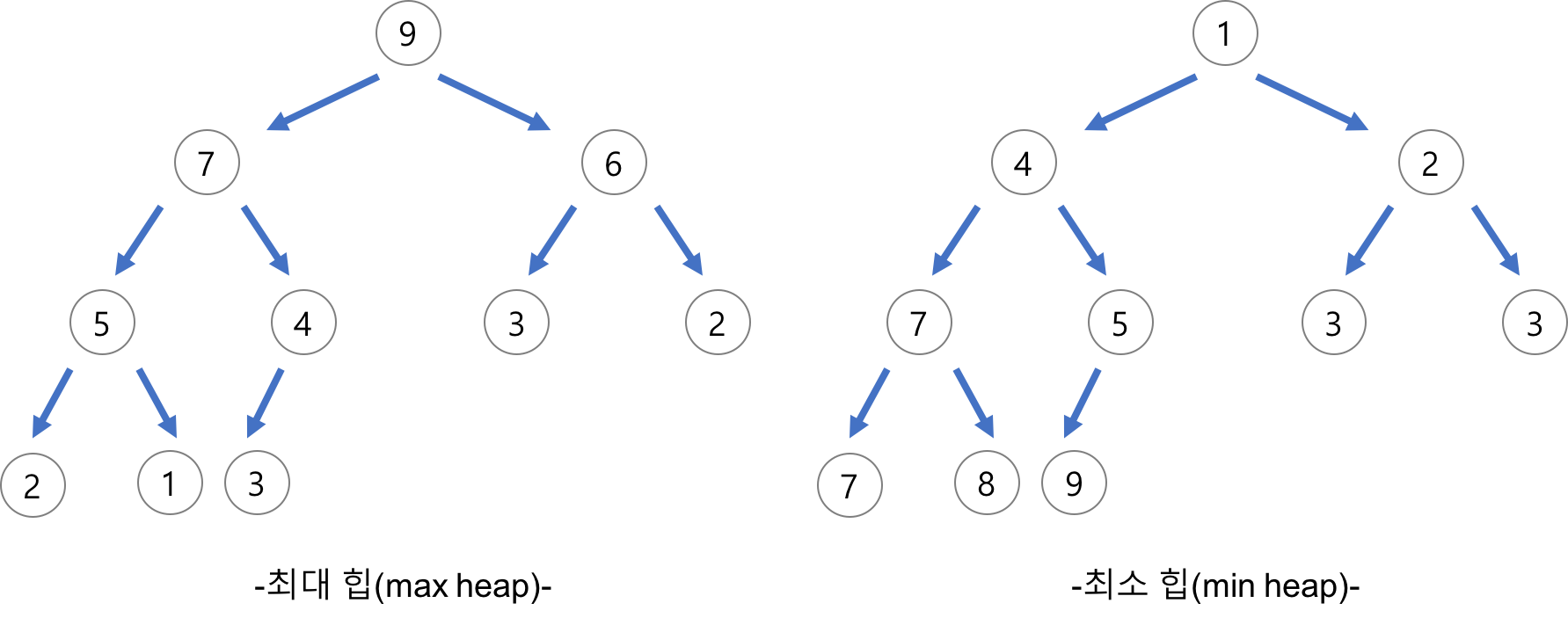
힙(heap)은 최댓값과 최솟값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)이다.
어떤 정수형 배열이 있다고 가정해보자.
[9, 8, 7, 6, 5, 4, 3, 2, 1]
이 배열에서 가장 작은 값을 꺼내오려면 요소 하나씩을 검색해서 찾아내야 한다. 그렇게 되면 시간복잡도는 O(n)이 된다. 해당 배열을 힙으로 구현한다면 O(log n)의 시간복잡도를 갖게 된다. 위에서 말했듯이 힙은 완전 이진 트리로 이루어져있기 때문이다.
완전 이진 트리는 마지막 노드를 제외한 모든 노드가 채워져있는 트리의 한 종류로, 배열을 아주 효율적으로 표현해주는 트리이다. 완전 이진 트리를 사용하는 힙 역시 효율성이 좋아서 다양한 분야에서 널리 사용되고 있는데, 대표적으로는 우선순위 큐에서 활용되고 있다.
힙의 특징은 다음과 같다
- 최소 힙에서는 부모가 항상 자식보다 작거나 같다.
- 최대 힙에서는 부모가 항상 자식보다 크거나 같다.
- 힙에서는 중복값을 허용한다. 힙은 최댓값 또는 최솟값을 쉽게 뽑기 위한 자료구조이기 때문이다.
여기서 알아둬야하는 점은 힙은 정렬된 구조가 아니라는 점이다.
최소 힙이든 최대 힙이든 부모, 자식 간의 관계만 존재할 뿐 서로 정렬되어 있지는 않다. 그리고, 계산의 편의성과 가독성을 위해 인덱스를 1부터 사용한다. 이는 필수는 아니지만 일반적으로 이와 같이 사용하는 데에는 이유가 있기 때문이라고 생각한다. 나와 같은 초보는 일단 외우고 본다
이진 탐색 트리와 다른 점?
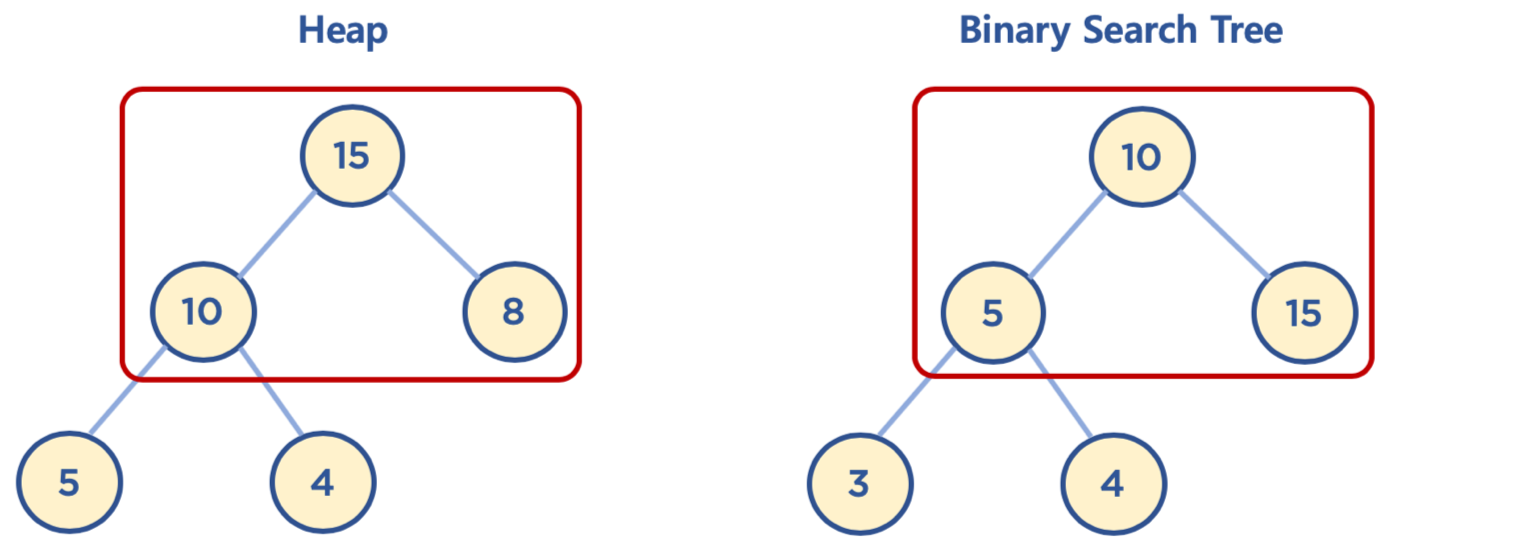
위에서 말했듯이 힙은 부모 노드가 자식노드보다 크거나(최대 힙), 작아야(최소 힙)한다.
반면 이진 탐색 트리는 부모 노드가 왼쪽 노드보다 크고, 오른쪽 노드보다 작아야한다는 조건이 있다.
이진 탐색 트리는 ‘탐색’을 위한, 힙은 ‘최대/최솟값 검색’을 위한 자료구조로 생각하면 된다.
힙 구현
힙은 언급했듯이 완전 이진 트리로 이루어져있기 때문에 배열을 가지고 쉽게 구현할 수 있다. 완전 이진 트리의 특성상 왼쪽부터 오른쪽으로 차곡차곡 노드가 저장되므로 배열의 구조를 사용할 수 있게 된다.
파이썬에는 편리하게도 힙 모듈을 지원해주지만, 힙이 어떻게 동작하는 지 아는 것은 중요하므로 그림과 함께 살펴보도록 하자. 최소와 최대 힙 구현 방식은 크게 다르지 않기 때문에 이 포스팅에서는 최소 힙을 선택해서 구현해보자.
삽입
위에서 말했듯이 파이썬에서는 힙 모듈을 지원해주기 때문에 실제로 사용한다기보단 어떤 방식으로 힙이 작동하는 지 흐름을 파악하는 방식으로 따라가자.
힙 모듈에 관한 공식 문서는 링크로 첨부해놓을테니 참고해보자!
https://www.daleseo.com/python-heapq/
[파이썬] heapq 모듈 사용법
Engineering Blog by Dale Seo
www.daleseo.com
아래는 삽입 과정을 그린 그림이다.
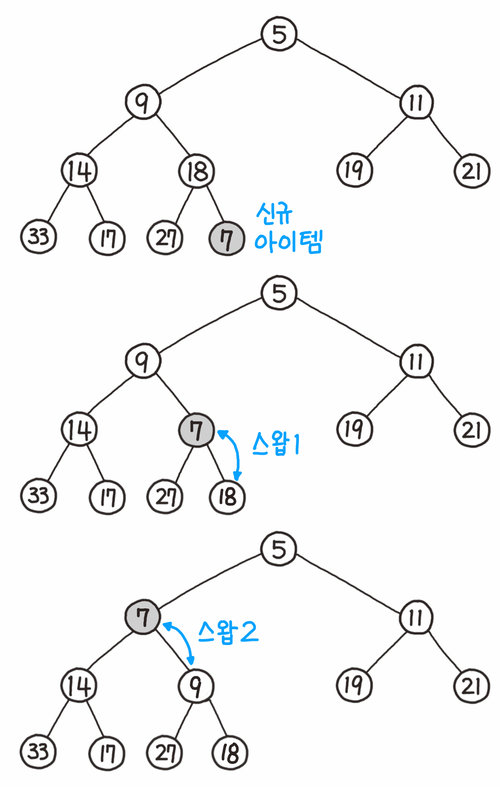
- 가장 끝의 자리에 노드를 삽입한다.
- 그 노드와 부모 노드를 서로 비교해서 삽입한 노드가 부모 노드보다 작다면 스왑해준다.
- 조건을 만족할 때까지 2번 과정을 반복한다.
위의 과정을 코드로 살펴보자
# 생성자와 len() 생략
# 삽입 함수
def insert(self, k):
# 힙 트리에 k값을 넣어준다. 가장 뒤에 들어가게 되므로 비교 연산 후 위치를 지정해준다.
self.items.append(k)
self._percolate_up()
# 노드를 위로 올려주는 함수
def _percolate_up(self):
# 현재 인덱스를 가장 마지막 인덱스 지정
cur = len(self)
# 부모의 왼쪽 자식 노드는 2*cur, 오른쪽 자식 노드는 2*cur+1이므로 부모노드는 항상 cur//2이다.
parent = cur // 2
while parent > 0:
# 현재 노드가 부모 노드보다 작다면 위치를 바꿔준다.
if self.items[cur] < self.items[parent]:
self.items[cur], self.items[parent] = self.items[parent], self.items[cur]
# 다음 비교를 위해 현재 인덱스는 우리가 방금 비교한 부모 인덱스인 parent로, parent는 새롭게 비교할 부모 인덱스로 바꿔준다.
cur = parent
parent = cur // 2
percolate_up() 함수를 위주로 살펴보자
가장 먼저 현재 인덱스를 가장 마지막 인덱스인 self의 길이로 지정해준다.
부모와 자식 노드의 인덱스는 그림을 통해 직관적으로 이해할 수 있는데, 부모 노드는 자식 노드를 2로 나눈 몫이 되고 왼쪽 자식 노드는 부모 노드 * 2, 오른쪽 자식 노드는 부모노드 * 2 + 1이 된다.
예를 들어, 가장 위 부모 노드의 인덱스는 1이고, 왼쪽 자식 노드의 인덱스는 2, 오른쪽 자식 노드의 인덱스는 3이다.
그 다음부터는 while문을 돌면서 삽입된 현재 노드의 값이 부모 노드보다 작을 때 스왑을 해주는 과정의 반복이다. if문 부분을 읽어보면 어렵지 않게 이해가 될 것이다.
한번의 스왑이 이루어지면 이제 현재 가르키고 있는 노드의 인덱스를 우리가 방금 비교한 부모 인덱스인 parent로, parent는 새롭게 비교할 부모 인덱스로 바꿔주고 while문을 반복한다. cur을 parent로 바꾸는 부분이 잘 이해가 안갔었는데 역시 그림과 함께보면 이해하기 쉽다.
삽입된 노드가 스왑을 통해 한 칸 위로 올라갔기 때문에 인덱스 역시 같이 한 칸 올라가야하고, 그게 방금 우리가 비교한 부모 인덱스인 parent와 같다는 말이다.
while문을 계속 돌리다보면 결국 현재 인덱스가 0이 되는 순간이 오게 되는데, 이 지점에 다다르면 끝이 나게 된다.
삭제
힙 삭제는 삽입보다는 약간 어렵다. 하지만 그림으로 보면서 천천히 따라가다보면 이해가 되는 순간이 오게 되니 그림과 함께 보자!
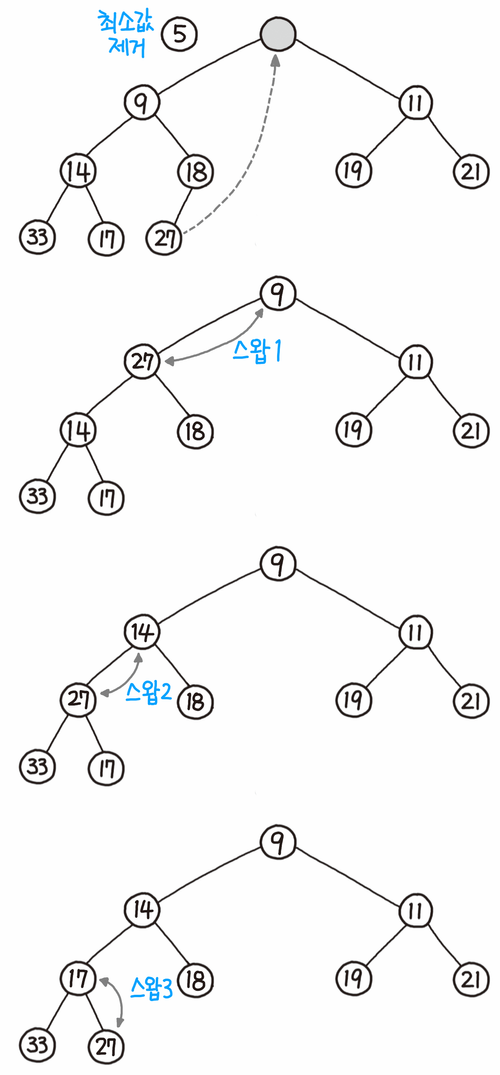
- 루트 노드를 제거한다.
- 루트 자리에 가장 마지막 노드를 삽입한다.
- 올라간 노드와 그의 자식 노드을 비교해서 삽입한 노드보다 더 작은 자식이 있다면 그대로 두고 그렇지 않으면 스왑해준다. 이때, 삽입한 노드보다 더 작은 자식이 둘이라면 자식들 중 작은 값과 스왑한다.
- 조건을 만족할 때까지 3의 과정을 반복한다.
결국에는 최소 힙에서 가장 작은 값을 뽑아내고, 마지막에 있는 노드를 규칙에 맞게 하나씩 아래로 내리는 과정의 반복이다. 이번에도 코드를 살펴보자.
주석이 길게 써있어서 복잡해보이지만 짧은 코드이다
# 생성자와 len() 생략
# 추출 함수
def extract(self):
# 예외 처리. 힙이 비어있을 때 None을 리턴한다.
if len(self) < 1:
return None
# __init__ 함수에서 가장 첫번째 인덱스를 1로 하기로 했으므로 루트 노드는 1번째 인덱스에 들어가게 된다.
root = self.items[1]
# 가장 첫번째 노드와 가장 마지막 노드를 바꿔준다. 힙에서 pop을 하면 가장 마지막 노드가 뽑혀나오기 때문.
# 힙은 root노드만 pop 할 수 있다.
self.items[1] = self.items[-1]
# 맨 뒤로 옮겨준 root 노드를 추출한다
self.items.pop()
# 처음에 root노드와 바꾼 마지막 노드를 비교해서 적절한 위치에 배치해준다.
self._percolate_down(1)
# 어떻게 root노드를 pop했는데 다시 반환할 수 있죠?
# 가장 처음에 우린 root 노드를 변수에 담아줬기 때문에 pop을 했더라도 이미 root 변수에 저장되어있다.
return root
# 노드를 아래로 내려주는 함수
def _percolate_down(self, cur):
# 왼쪽 자식은 부모 노드 * 2, 오른쪽자식은 부모 노드 * 2 + 1
left = cur * 2
right = cur * 2 + 1
# 우선 최소값을 현재 가리키고 있는 노드의 인덱스로 지정해준다.
smallest = cur
# 왼쪽 자식 노드와 비교.
# left가 트리 안에 있으면서, 현재 가리키고 있는 노드보다 작으면 최소값을 가리키는 인덱스를 left로 바꿔준다.
if left <= len(self) and self.items[left] < self.items[smallest]:
smallest = left
# 오른쪽 자식 노드와 비교.
# left와 같은 방식이다.
if right <= len(self) and self.items[right] < self.items[smallest]:
smallest = right
# smallest의 인덱스가 바뀌었다면 (자식 노드에 더 작은 값이 존재한다면) 스왑해준다.
if smallest != cur:
self.items[cur], self.items[smallest] = self.items[smallest], self.items[cur]
# 재귀 호출로 반복
self._percolate_down(smallest)
삽입하는 과정과 비슷하면서 반대로 진행되는 느낌이다. 사실 코드를 보면 위에 그림에서 설명했던 과정과 크게 다르지 않다.
extract() 함수에서 추출할 최소값인 root 노드를 리턴해주기 위해 우선 변수에 담아주고, 마지막 노드와 뒤바꿔준다. 그러고 나서 root 노드를 제거해준다음 바꿔준 마지막 노드를 차근차근 아래로 내려주면 된다.
_percolate_down() 함수는 뒤바뀐 마지막 노드를 다시 규칙에 맞게 정렬해주는 함수로, 이 역시 _percolate_up()와 크게 차이가 나지는 않는다. 다른 점이라면 최소값인 smallest의 인덱스를 현재 가리키고 있는 인덱스로 지정해준 다음 왼쪽 자식 노드와 오른쪽 자식 노드와 비교해보고 둘 중 더 작은 쪽 인덱스를 smallest에 넣어주는 부분이다.
이렇게 힙의 삽입과 추출 구현을 해보았다! 다시한 번 언급하지만 파이썬에는 힙 모듈이 있으므로 구현은 흐름을 익히는 용도로 사용하고 모듈도 사랑해주자
문제풀이
[leetcode] 1464. 배열에 있는 두 요소의 최대 곱 (Maximum Product of Two Elements in an Array)
[leetcode] 1464. 배열에 있는 두 요소의 최대 곱 (Maximum Product of Two Elements in an Array)
들어가며 본 포스팅은 <파이썬 알고리즘 인터뷰> 책에서 다룬 리트코드 문제들을 다루고 있습니다. 문제들은 모두 리트코드에서 출제된 문제들이며, 문제 풀이의 많은 부분을 책의 힌트와 해설
annajin.tistory.com
새로 알게 된 것 - 최소 힙을 튜플을 이용하여 최대 힙으로 만들기
마치며
오늘의 한마디 by 건우님 - 쉽다고 자만하지 말자!
매일 TIL에 항해99 수강생 분들의 오늘의 한마디를 적기로 했다. 의미가 깊을 것 같아서 시작했는데 수료 후에 보면 기분이 색다를 것 같다!
오늘도 고생했습니다!
출처
[자료구조] 그림으로 쉽게 보는 힙(HEAP) 개념과 코드
'Study > TIL' 카테고리의 다른 글
| [TIL] 05/27 항해99 19일차 - 퀵/병합 정렬 (0) | 2022.05.27 |
|---|---|
| [TIL] 05/26 항해99 18일차 - 버블/선택/삽입 정렬, 문제풀이 (0) | 2022.05.27 |
| [TIL] 05/24 항해99 16일차 - 이진탐색트리, 문제풀이 (0) | 2022.05.24 |
| [TIL] 05/23 항해99 15일차 - 트리, 이진 트리, 문제풀이 (1) | 2022.05.24 |
| [TIL] 05/21 항해99 13일차 - 보안 공격, 백트래킹, 문제풀이 (0) | 2022.05.22 |

들어가며
나에게 맞는 알고리즘 공부 방법을 찾고나니 한결 마음이 가벼워졌다. 또, 오늘은 문제가 쉬웠는지 직접 문제 풀이에 성공해서 꽤나 뿌듯했다.
이 기쁜 마음을 안고, 오늘의 TIL은 힙의 개념과 문제풀이, 새로 알게 된 개념을 정리해보고자 한다.
힙
힙(heap)은 최댓값과 최솟값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)이다.

어떤 정수형 배열이 있다고 가정해보자.
[9, 8, 7, 6, 5, 4, 3, 2, 1]
이 배열에서 가장 작은 값을 꺼내오려면 요소 하나씩을 검색해서 찾아내야 한다. 그렇게 되면 시간복잡도는 O(n)이 된다. 해당 배열을 힙으로 구현한다면 O(log n)의 시간복잡도를 갖게 된다. 위에서 말했듯이 힙은 완전 이진 트리로 이루어져있기 때문이다.
완전 이진 트리는 마지막 노드를 제외한 모든 노드가 채워져있는 트리의 한 종류로, 배열을 아주 효율적으로 표현해주는 트리이다. 완전 이진 트리를 사용하는 힙 역시 효율성이 좋아서 다양한 분야에서 널리 사용되고 있는데, 대표적으로는 우선순위 큐에서 활용되고 있다.
힙의 특징은 다음과 같다
- 최소 힙에서는 부모가 항상 자식보다 작거나 같다.
- 최대 힙에서는 부모가 항상 자식보다 크거나 같다.
- 힙에서는 중복값을 허용한다. 힙은 최댓값 또는 최솟값을 쉽게 뽑기 위한 자료구조이기 때문이다.
여기서 알아둬야하는 점은 힙은 정렬된 구조가 아니라는 점이다.
최소 힙이든 최대 힙이든 부모, 자식 간의 관계만 존재할 뿐 서로 정렬되어 있지는 않다. 그리고, 계산의 편의성과 가독성을 위해 인덱스를 1부터 사용한다. 이는 필수는 아니지만 일반적으로 이와 같이 사용하는 데에는 이유가 있기 때문이라고 생각한다. 나와 같은 초보는 일단 외우고 본다
이진 탐색 트리와 다른 점?

위에서 말했듯이 힙은 부모 노드가 자식노드보다 크거나(최대 힙), 작아야(최소 힙)한다.
반면 이진 탐색 트리는 부모 노드가 왼쪽 노드보다 크고, 오른쪽 노드보다 작아야한다는 조건이 있다.
이진 탐색 트리는 ‘탐색’을 위한, 힙은 ‘최대/최솟값 검색’을 위한 자료구조로 생각하면 된다.
힙 구현
힙은 언급했듯이 완전 이진 트리로 이루어져있기 때문에 배열을 가지고 쉽게 구현할 수 있다. 완전 이진 트리의 특성상 왼쪽부터 오른쪽으로 차곡차곡 노드가 저장되므로 배열의 구조를 사용할 수 있게 된다.
파이썬에는 편리하게도 힙 모듈을 지원해주지만, 힙이 어떻게 동작하는 지 아는 것은 중요하므로 그림과 함께 살펴보도록 하자. 최소와 최대 힙 구현 방식은 크게 다르지 않기 때문에 이 포스팅에서는 최소 힙을 선택해서 구현해보자.
삽입
위에서 말했듯이 파이썬에서는 힙 모듈을 지원해주기 때문에 실제로 사용한다기보단 어떤 방식으로 힙이 작동하는 지 흐름을 파악하는 방식으로 따라가자.
힙 모듈에 관한 공식 문서는 링크로 첨부해놓을테니 참고해보자!
https://www.daleseo.com/python-heapq/
[파이썬] heapq 모듈 사용법
Engineering Blog by Dale Seo
www.daleseo.com
아래는 삽입 과정을 그린 그림이다.

- 가장 끝의 자리에 노드를 삽입한다.
- 그 노드와 부모 노드를 서로 비교해서 삽입한 노드가 부모 노드보다 작다면 스왑해준다.
- 조건을 만족할 때까지 2번 과정을 반복한다.
위의 과정을 코드로 살펴보자
# 생성자와 len() 생략
# 삽입 함수
def insert(self, k):
# 힙 트리에 k값을 넣어준다. 가장 뒤에 들어가게 되므로 비교 연산 후 위치를 지정해준다.
self.items.append(k)
self._percolate_up()
# 노드를 위로 올려주는 함수
def _percolate_up(self):
# 현재 인덱스를 가장 마지막 인덱스 지정
cur = len(self)
# 부모의 왼쪽 자식 노드는 2*cur, 오른쪽 자식 노드는 2*cur+1이므로 부모노드는 항상 cur//2이다.
parent = cur // 2
while parent > 0:
# 현재 노드가 부모 노드보다 작다면 위치를 바꿔준다.
if self.items[cur] < self.items[parent]:
self.items[cur], self.items[parent] = self.items[parent], self.items[cur]
# 다음 비교를 위해 현재 인덱스는 우리가 방금 비교한 부모 인덱스인 parent로, parent는 새롭게 비교할 부모 인덱스로 바꿔준다.
cur = parent
parent = cur // 2
percolate_up() 함수를 위주로 살펴보자
가장 먼저 현재 인덱스를 가장 마지막 인덱스인 self의 길이로 지정해준다.
부모와 자식 노드의 인덱스는 그림을 통해 직관적으로 이해할 수 있는데, 부모 노드는 자식 노드를 2로 나눈 몫이 되고 왼쪽 자식 노드는 부모 노드 * 2, 오른쪽 자식 노드는 부모노드 * 2 + 1이 된다.
예를 들어, 가장 위 부모 노드의 인덱스는 1이고, 왼쪽 자식 노드의 인덱스는 2, 오른쪽 자식 노드의 인덱스는 3이다.
그 다음부터는 while문을 돌면서 삽입된 현재 노드의 값이 부모 노드보다 작을 때 스왑을 해주는 과정의 반복이다. if문 부분을 읽어보면 어렵지 않게 이해가 될 것이다.
한번의 스왑이 이루어지면 이제 현재 가르키고 있는 노드의 인덱스를 우리가 방금 비교한 부모 인덱스인 parent로, parent는 새롭게 비교할 부모 인덱스로 바꿔주고 while문을 반복한다. cur을 parent로 바꾸는 부분이 잘 이해가 안갔었는데 역시 그림과 함께보면 이해하기 쉽다.
삽입된 노드가 스왑을 통해 한 칸 위로 올라갔기 때문에 인덱스 역시 같이 한 칸 올라가야하고, 그게 방금 우리가 비교한 부모 인덱스인 parent와 같다는 말이다.
while문을 계속 돌리다보면 결국 현재 인덱스가 0이 되는 순간이 오게 되는데, 이 지점에 다다르면 끝이 나게 된다.
삭제
힙 삭제는 삽입보다는 약간 어렵다. 하지만 그림으로 보면서 천천히 따라가다보면 이해가 되는 순간이 오게 되니 그림과 함께 보자!

- 루트 노드를 제거한다.
- 루트 자리에 가장 마지막 노드를 삽입한다.
- 올라간 노드와 그의 자식 노드을 비교해서 삽입한 노드보다 더 작은 자식이 있다면 그대로 두고 그렇지 않으면 스왑해준다. 이때, 삽입한 노드보다 더 작은 자식이 둘이라면 자식들 중 작은 값과 스왑한다.
- 조건을 만족할 때까지 3의 과정을 반복한다.
결국에는 최소 힙에서 가장 작은 값을 뽑아내고, 마지막에 있는 노드를 규칙에 맞게 하나씩 아래로 내리는 과정의 반복이다. 이번에도 코드를 살펴보자.
주석이 길게 써있어서 복잡해보이지만 짧은 코드이다
# 생성자와 len() 생략
# 추출 함수
def extract(self):
# 예외 처리. 힙이 비어있을 때 None을 리턴한다.
if len(self) < 1:
return None
# __init__ 함수에서 가장 첫번째 인덱스를 1로 하기로 했으므로 루트 노드는 1번째 인덱스에 들어가게 된다.
root = self.items[1]
# 가장 첫번째 노드와 가장 마지막 노드를 바꿔준다. 힙에서 pop을 하면 가장 마지막 노드가 뽑혀나오기 때문.
# 힙은 root노드만 pop 할 수 있다.
self.items[1] = self.items[-1]
# 맨 뒤로 옮겨준 root 노드를 추출한다
self.items.pop()
# 처음에 root노드와 바꾼 마지막 노드를 비교해서 적절한 위치에 배치해준다.
self._percolate_down(1)
# 어떻게 root노드를 pop했는데 다시 반환할 수 있죠?
# 가장 처음에 우린 root 노드를 변수에 담아줬기 때문에 pop을 했더라도 이미 root 변수에 저장되어있다.
return root
# 노드를 아래로 내려주는 함수
def _percolate_down(self, cur):
# 왼쪽 자식은 부모 노드 * 2, 오른쪽자식은 부모 노드 * 2 + 1
left = cur * 2
right = cur * 2 + 1
# 우선 최소값을 현재 가리키고 있는 노드의 인덱스로 지정해준다.
smallest = cur
# 왼쪽 자식 노드와 비교.
# left가 트리 안에 있으면서, 현재 가리키고 있는 노드보다 작으면 최소값을 가리키는 인덱스를 left로 바꿔준다.
if left <= len(self) and self.items[left] < self.items[smallest]:
smallest = left
# 오른쪽 자식 노드와 비교.
# left와 같은 방식이다.
if right <= len(self) and self.items[right] < self.items[smallest]:
smallest = right
# smallest의 인덱스가 바뀌었다면 (자식 노드에 더 작은 값이 존재한다면) 스왑해준다.
if smallest != cur:
self.items[cur], self.items[smallest] = self.items[smallest], self.items[cur]
# 재귀 호출로 반복
self._percolate_down(smallest)
삽입하는 과정과 비슷하면서 반대로 진행되는 느낌이다. 사실 코드를 보면 위에 그림에서 설명했던 과정과 크게 다르지 않다.
extract() 함수에서 추출할 최소값인 root 노드를 리턴해주기 위해 우선 변수에 담아주고, 마지막 노드와 뒤바꿔준다. 그러고 나서 root 노드를 제거해준다음 바꿔준 마지막 노드를 차근차근 아래로 내려주면 된다.
_percolate_down() 함수는 뒤바뀐 마지막 노드를 다시 규칙에 맞게 정렬해주는 함수로, 이 역시 _percolate_up()와 크게 차이가 나지는 않는다. 다른 점이라면 최소값인 smallest의 인덱스를 현재 가리키고 있는 인덱스로 지정해준 다음 왼쪽 자식 노드와 오른쪽 자식 노드와 비교해보고 둘 중 더 작은 쪽 인덱스를 smallest에 넣어주는 부분이다.
이렇게 힙의 삽입과 추출 구현을 해보았다! 다시한 번 언급하지만 파이썬에는 힙 모듈이 있으므로 구현은 흐름을 익히는 용도로 사용하고 모듈도 사랑해주자
문제풀이
[leetcode] 1464. 배열에 있는 두 요소의 최대 곱 (Maximum Product of Two Elements in an Array)
[leetcode] 1464. 배열에 있는 두 요소의 최대 곱 (Maximum Product of Two Elements in an Array)
들어가며 본 포스팅은 <파이썬 알고리즘 인터뷰> 책에서 다룬 리트코드 문제들을 다루고 있습니다. 문제들은 모두 리트코드에서 출제된 문제들이며, 문제 풀이의 많은 부분을 책의 힌트와 해설
annajin.tistory.com
새로 알게 된 것 - 최소 힙을 튜플을 이용하여 최대 힙으로 만들기
마치며
오늘의 한마디 by 건우님 - 쉽다고 자만하지 말자!
매일 TIL에 항해99 수강생 분들의 오늘의 한마디를 적기로 했다. 의미가 깊을 것 같아서 시작했는데 수료 후에 보면 기분이 색다를 것 같다!
오늘도 고생했습니다!
출처
[자료구조] 그림으로 쉽게 보는 힙(HEAP) 개념과 코드
'Study > TIL' 카테고리의 다른 글
| [TIL] 05/27 항해99 19일차 - 퀵/병합 정렬 (0) | 2022.05.27 |
|---|---|
| [TIL] 05/26 항해99 18일차 - 버블/선택/삽입 정렬, 문제풀이 (0) | 2022.05.27 |
| [TIL] 05/24 항해99 16일차 - 이진탐색트리, 문제풀이 (0) | 2022.05.24 |
| [TIL] 05/23 항해99 15일차 - 트리, 이진 트리, 문제풀이 (1) | 2022.05.24 |
| [TIL] 05/21 항해99 13일차 - 보안 공격, 백트래킹, 문제풀이 (0) | 2022.05.22 |
