
들어가며
TIL을 쓰려고 보니 새삼 벌써 항해99에 승선한 지 19일 밖에 지나지 않았다는 사실을 깨달았다. 체감상 알고리즘 주차가 시작된지 한달은 족히 된거같은데 아직 한주가 더 남았다니... 이제 슬슬 체력이 딸리기 시작했다. 최근 며칠간 TIL을 쓸 기력이 없어서 대충 쓴 느낌이 컸는데, 오늘도 아마 비슷할 것 같다. 이번 주 일요일에 푹 쉬어서 체력을 보충해야겠다.
넋두리는 이정도로 하고, 오늘의 TIL은 강의 진도에 맞게 퀵 정렬과 병합 정렬의 개념을 정리하고자 한다.
정렬
퀵 정렬
퀵정렬(Quick sort)은 이름에서 알 수 있다시피 O(n log n)이라는 빠른 속도로 정렬할 수 있는 알고리즘이다. 퀵 정렬은 분할 정복(Divide and Conquert)를 통해 정렬을 하게 되는데, 기준(pivot)을 잡고, 재귀 구조를 이용해 기준보다 작은 집합과 큰 집합으로 나누어 정렬하는 방식이다.
분할 정복(Divide and Conquert)?
그대로 해결할 수 없는 문제를 작은 문제로 분할하여 해결하는 방법이나 알고리즘을 말한다. 일반적으로 재귀를 통해 구현된다.
앗 그럼 퀵 정렬이 항상 빠른건가요?라고 물으신다면 대답해 드리는게 인지상정
‘퀵’ 정렬이라고 해서 항상 빠른 건 아니다. 만약 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 같이 기준이 좌/우로 나누지 못하는 최악의 상황이라면 시간 복잡도는 O(n^2)이 된다. 최악의 상황일 때 총 연산 횟수가 무려 25억번이 된다고 한다.
추가로 퀵 정렬은 불안정(Unstable) 정렬이라 안정 정렬(Stable) 정렬을 사용하는 파이썬은 퀵 정렬을 하지 않는다고 한다.
안정 정렬(Stable), 불안정(Unstable) 정렬?
중복된 값이 존재하는 데이터를 정렬할 때, 중복된 값을 기존에 입력되어있는 순서와 똑같이 정렬하면 안정 정렬, 순서에 상관없이 정렬하면 불안정 정렬이다.
퀵 정렬을 예시로 설명해주는 블로그가 있어서 첨부하니 흐름이 이해되지 않는다면 참고하도록 하자. 이 블로그는 자바로 구현되어있다.
퀵 정렬 (Quick sort) 쉽게 알기
퀵 정렬(Quick sort) 퀵 정렬은 평균적으로 매우 빠른 속도를 자랑하는 정렬 방법입니다. 그렇기에 이름부터가 다소 건방진 '퀵' 정렬인데요. 보통 다른 정렬 방법들은 이름으로부터 어떻게 정렬을
spacebike.tistory.com
퀵 정렬 구현하기
이제 퀵 정렬을 코드와 함께 이해해보자.
def quick_sort(lst, start, end):
def partition(part, ps, pe):
# 기준점을 가장 오른쪽 요소로 잡는다.
pivot = part[pe]
# pivot보다 작은 집합의 인덱스 i를 -1로 잡아둔다.
i = ps - 1
# 정렬하려는 집합의 범위 [ps:pe]
for j in range(ps, pe):
# pivot보다 작은 값을 발견했다면 왼쪽 집합으로 나열해줘야햐므로
# i 인덱스의 요소와 현재 가리키고 있는 j 인덱스의 요소를 바꿔준다.
if part[j] <= pivot:
i += 1
part[i], part[j] = part[j], part[i]
# pivot보다 더 큰 값이 되는 부분인 i + 1과 pivot의 요소를 바꿔준다.
part[i + 1], part[pe] = part[pe], part[i + 1]
return i + 1
# 예외 처리
if start >= end:
return None
# 왼쪽과 오른쪽 집합으로 나눠주는 기준을 만들어주는 함수
p = partition(lst, start, end)
# pivot의 왼쪽 집합 재귀
quick_sort(lst, start, p - 1)
# pivot의 오른쪽 집합 재귀
quick_sort(lst, p + 1, end)
return lst
partition() 함수를 보기 전에 quick_sort() 함수로 재귀가 어떻게 진행되는 지 확인해보자
가장 먼저 나오는 건 예외 처리이다. start는 왼쪽, end는 오른쪽 인덱스로 범위를 지정해주는데 이 두개가 같거나, start가 더 커지면 더 이상 검색할 범위가 없어지므로 종료한다.
partition() 함수는 퀵 정렬의 방식대로 기준점의 좌/우로 나누기 위한 기준을 만들어주는 함수이다. 아래의 그림처럼 pivot을 만들어주고 이를 다음 재귀를 위해 변수에 담아준다.
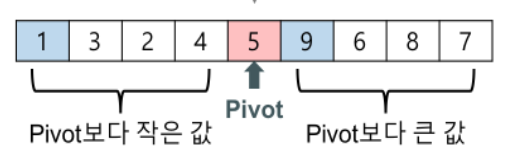
그리고 나서 pivot보다 작은 값의 집합과 큰 값의 집합을 각각 다시 퀵 정렬해주는 재귀 함수를 호출한다. 여기서 pivot보다 작은 값의 집합은 0번째 인덱스부터 pivot의 - 1번째 인덱스의 범위이고, pivot보다 큰 값의 집합은 pivot의 + 1번째 인덱스부터 마지막 인덱스의 범위이다.
이제 partition() 함수를 살펴보자
def partition(part, ps, pe):
# 기준점을 가장 오른쪽 요소로 잡는다.
pivot = part[pe]
# pivot보다 작은 집합의 인덱스 i를 -1로 잡아둔다.
i = ps - 1
# 정렬하려는 집합의 범위 [ps:pe]
for j in range(ps, pe):
# pivot보다 작은 값을 발견했다면 왼쪽 집합으로 나열해줘야햐므로
# i 인덱스의 요소와 현재 가리키고 있는 j 인덱스의 요소를 바꿔준다.
if part[j] <= pivot:
i += 1
part[i], part[j] = part[j], part[i]
# pivot보다 더 큰 값이 되는 부분인 i + 1과 pivot의 요소를 바꿔준다.
part[i + 1], part[pe] = part[pe], part[i + 1]
return i + 1
우선 pivot을 배열의 가장 마지막 요소로 잡아둔다. 이 값을 앞의 요소들과 비교하면서 적절한 위치에 넣어줄 것이다.
i는 pivot보다 작은 집합의 인덱스를 표시하는데, 가장 처음에는 존재하지 않기 때문에 -1을 해주고 점점 범위를 늘려가준다. pivot보다 작은 값을 발견했을 때 쓰인다.
이제 정렬하려는 집합의 범위 만큼 for문을 돌려주는데, 현재 가리키는 포인터인 j 인덱스의 요소가 pivot보다 작으면 왼쪽으로 보내주고, i를 + 1 시켜줌으로써 pivot보다 작은 값의 집합을 만들어준다.
최종적으로 pivot의 왼쪽과 오른쪽으로 정렬이 완료되었다면 기준점을 왼쪽과 오른쪽의 가운데로 옮겨주고, 기준점의 인덱스인 i + 1을 리턴해준다.
위의 과정을 계속 반복하다보면 최종적으로 정렬된 배열을 리턴하고 퀵 정렬이 종료된다.
병합 정렬
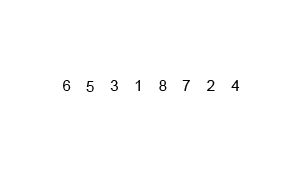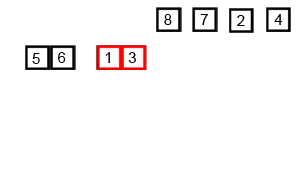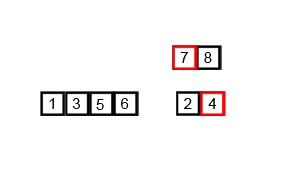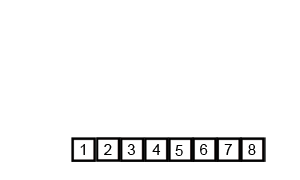
병합 정렬(= 합병정렬, Merge sort)은 퀵 정렬과 마찬가지로 분할 정복을 통해 정렬하는 방식이다. 주어진 배열을 반으로 쪼개는 과정을 반복해서 최대한으로 쪼갠 후, 분할이 끝나면 정렬을 하면서 병합(merge)를 하는 방식이다.
퀵 정렬과 비교해서 병합 정렬의 속도는 대부분의 경우 느리지만, 어떤 경우에도 O(n log n)이라는 일정한 속도를 내고, 안정 정렬이라는 점에서 상용 라이브러리에 많이 사용되고 있다.
병합 정렬 구현하기
병합 정렬은 merge하는 함수와 배열을 쪼개주는 함수 두가지를 이용한다.
def merge(arr1, arr2):
# 결과를 담아줄 빈 배열
result = []
# 하나씩 선택할 포인터
i = j = 0
# 각각 비교 후 result에 담아준다
while i < len (arr1) and j < len(arr2):
if arr1[i] < arr2[j]:
result.append(arr1[i])
i += 1
else:
result.append(arr2[j])
j += 1
# 비교가 끝나고 남은 요소들 result에 삽입
while i < len(arr1):
result.append(arr1[i])
i += 1
while j < len(arr2):
result.append(arr2[j])
j += 1
return result
쪼개준 배열을 정렬해서 다시 합쳐주기 위한 함수이다.
구현하는 방식은 개념을 이해하면 크게 어렵지 않다. while문을 돌리기 때문에 i와 j를 따로 선언해주고, i와 j 포인터가 배열의 끝에 다다를 때까지 반복한다. 배열1과 배열2의 요소 중 더 큰 값을 result 리스트에 넣어주고, 마지막에 남은 요소들을 하나씩 result에 넣어주면 끝이다. 간단하쥬?
def merge_sort(lst):
# 예외 처리
if len(lst) <= 1:
return lst
# 재귀를 이용하여 리스트를 끝까지 쪼개준다.
mid = len(lst) // 2
L = merge_sort(lst[:mid])
R = merge_sort(lst[mid:])
return merge(L, R)
배열을 쪼개주기 위한 함수도 크게 어렵지 않다. 그저 중간 인덱스를 찾아 재귀 호출을 해서 계속 절반씩 쪼개주고, 재귀 구조의 가장 깊숙이까지 들어가서 모든 요소가 쪼개졌다면, 위에서 구현한 merge()함수를 이용해 정렬하고 다시 합쳐주는 과정만 반복해주면 된다.
마치며
평소에도 좋았던건 아니었지만 오늘 유독 공부가 손에 안잡혔다. 다른 때 같았으면 '그래도 해야지...' 하면서 억지로라도 했을 텐데 오늘은 그마저도 싫었다. 밥을 안먹어서 그런가... 오늘은 일찍 자야겠다.

'Study > TIL' 카테고리의 다른 글
| [TIL] 05/30 항해99 22일차 - 동기 & 비동기 (0) | 2022.05.31 |
|---|---|
| [TIL] 05/28 항해99 20일차 - 이진탐색 (0) | 2022.05.28 |
| [TIL] 05/26 항해99 18일차 - 버블/선택/삽입 정렬, 문제풀이 (0) | 2022.05.27 |
| [TIL] 05/25 항해99 17일차 - 힙, 문제풀이 (1) | 2022.05.26 |
| [TIL] 05/24 항해99 16일차 - 이진탐색트리, 문제풀이 (0) | 2022.05.24 |

들어가며
TIL을 쓰려고 보니 새삼 벌써 항해99에 승선한 지 19일 밖에 지나지 않았다는 사실을 깨달았다. 체감상 알고리즘 주차가 시작된지 한달은 족히 된거같은데 아직 한주가 더 남았다니... 이제 슬슬 체력이 딸리기 시작했다. 최근 며칠간 TIL을 쓸 기력이 없어서 대충 쓴 느낌이 컸는데, 오늘도 아마 비슷할 것 같다. 이번 주 일요일에 푹 쉬어서 체력을 보충해야겠다.
넋두리는 이정도로 하고, 오늘의 TIL은 강의 진도에 맞게 퀵 정렬과 병합 정렬의 개념을 정리하고자 한다.
정렬
퀵 정렬
퀵정렬(Quick sort)은 이름에서 알 수 있다시피 O(n log n)이라는 빠른 속도로 정렬할 수 있는 알고리즘이다. 퀵 정렬은 분할 정복(Divide and Conquert)를 통해 정렬을 하게 되는데, 기준(pivot)을 잡고, 재귀 구조를 이용해 기준보다 작은 집합과 큰 집합으로 나누어 정렬하는 방식이다.
분할 정복(Divide and Conquert)?
그대로 해결할 수 없는 문제를 작은 문제로 분할하여 해결하는 방법이나 알고리즘을 말한다. 일반적으로 재귀를 통해 구현된다.
앗 그럼 퀵 정렬이 항상 빠른건가요?라고 물으신다면 대답해 드리는게 인지상정
‘퀵’ 정렬이라고 해서 항상 빠른 건 아니다. 만약 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 같이 기준이 좌/우로 나누지 못하는 최악의 상황이라면 시간 복잡도는 O(n^2)이 된다. 최악의 상황일 때 총 연산 횟수가 무려 25억번이 된다고 한다.
추가로 퀵 정렬은 불안정(Unstable) 정렬이라 안정 정렬(Stable) 정렬을 사용하는 파이썬은 퀵 정렬을 하지 않는다고 한다.
안정 정렬(Stable), 불안정(Unstable) 정렬?
중복된 값이 존재하는 데이터를 정렬할 때, 중복된 값을 기존에 입력되어있는 순서와 똑같이 정렬하면 안정 정렬, 순서에 상관없이 정렬하면 불안정 정렬이다.
퀵 정렬을 예시로 설명해주는 블로그가 있어서 첨부하니 흐름이 이해되지 않는다면 참고하도록 하자. 이 블로그는 자바로 구현되어있다.
퀵 정렬 (Quick sort) 쉽게 알기
퀵 정렬(Quick sort) 퀵 정렬은 평균적으로 매우 빠른 속도를 자랑하는 정렬 방법입니다. 그렇기에 이름부터가 다소 건방진 '퀵' 정렬인데요. 보통 다른 정렬 방법들은 이름으로부터 어떻게 정렬을
spacebike.tistory.com
퀵 정렬 구현하기
이제 퀵 정렬을 코드와 함께 이해해보자.
def quick_sort(lst, start, end):
def partition(part, ps, pe):
# 기준점을 가장 오른쪽 요소로 잡는다.
pivot = part[pe]
# pivot보다 작은 집합의 인덱스 i를 -1로 잡아둔다.
i = ps - 1
# 정렬하려는 집합의 범위 [ps:pe]
for j in range(ps, pe):
# pivot보다 작은 값을 발견했다면 왼쪽 집합으로 나열해줘야햐므로
# i 인덱스의 요소와 현재 가리키고 있는 j 인덱스의 요소를 바꿔준다.
if part[j] <= pivot:
i += 1
part[i], part[j] = part[j], part[i]
# pivot보다 더 큰 값이 되는 부분인 i + 1과 pivot의 요소를 바꿔준다.
part[i + 1], part[pe] = part[pe], part[i + 1]
return i + 1
# 예외 처리
if start >= end:
return None
# 왼쪽과 오른쪽 집합으로 나눠주는 기준을 만들어주는 함수
p = partition(lst, start, end)
# pivot의 왼쪽 집합 재귀
quick_sort(lst, start, p - 1)
# pivot의 오른쪽 집합 재귀
quick_sort(lst, p + 1, end)
return lst
partition() 함수를 보기 전에 quick_sort() 함수로 재귀가 어떻게 진행되는 지 확인해보자
가장 먼저 나오는 건 예외 처리이다. start는 왼쪽, end는 오른쪽 인덱스로 범위를 지정해주는데 이 두개가 같거나, start가 더 커지면 더 이상 검색할 범위가 없어지므로 종료한다.
partition() 함수는 퀵 정렬의 방식대로 기준점의 좌/우로 나누기 위한 기준을 만들어주는 함수이다. 아래의 그림처럼 pivot을 만들어주고 이를 다음 재귀를 위해 변수에 담아준다.

그리고 나서 pivot보다 작은 값의 집합과 큰 값의 집합을 각각 다시 퀵 정렬해주는 재귀 함수를 호출한다. 여기서 pivot보다 작은 값의 집합은 0번째 인덱스부터 pivot의 - 1번째 인덱스의 범위이고, pivot보다 큰 값의 집합은 pivot의 + 1번째 인덱스부터 마지막 인덱스의 범위이다.
이제 partition() 함수를 살펴보자
def partition(part, ps, pe):
# 기준점을 가장 오른쪽 요소로 잡는다.
pivot = part[pe]
# pivot보다 작은 집합의 인덱스 i를 -1로 잡아둔다.
i = ps - 1
# 정렬하려는 집합의 범위 [ps:pe]
for j in range(ps, pe):
# pivot보다 작은 값을 발견했다면 왼쪽 집합으로 나열해줘야햐므로
# i 인덱스의 요소와 현재 가리키고 있는 j 인덱스의 요소를 바꿔준다.
if part[j] <= pivot:
i += 1
part[i], part[j] = part[j], part[i]
# pivot보다 더 큰 값이 되는 부분인 i + 1과 pivot의 요소를 바꿔준다.
part[i + 1], part[pe] = part[pe], part[i + 1]
return i + 1
우선 pivot을 배열의 가장 마지막 요소로 잡아둔다. 이 값을 앞의 요소들과 비교하면서 적절한 위치에 넣어줄 것이다.
i는 pivot보다 작은 집합의 인덱스를 표시하는데, 가장 처음에는 존재하지 않기 때문에 -1을 해주고 점점 범위를 늘려가준다. pivot보다 작은 값을 발견했을 때 쓰인다.
이제 정렬하려는 집합의 범위 만큼 for문을 돌려주는데, 현재 가리키는 포인터인 j 인덱스의 요소가 pivot보다 작으면 왼쪽으로 보내주고, i를 + 1 시켜줌으로써 pivot보다 작은 값의 집합을 만들어준다.
최종적으로 pivot의 왼쪽과 오른쪽으로 정렬이 완료되었다면 기준점을 왼쪽과 오른쪽의 가운데로 옮겨주고, 기준점의 인덱스인 i + 1을 리턴해준다.
위의 과정을 계속 반복하다보면 최종적으로 정렬된 배열을 리턴하고 퀵 정렬이 종료된다.
병합 정렬
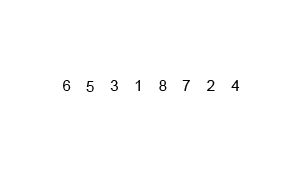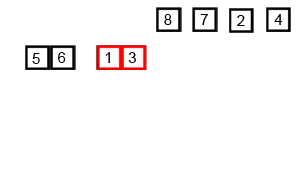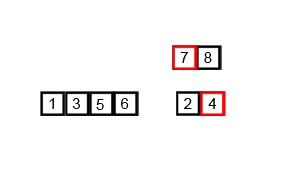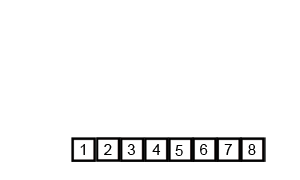
병합 정렬(= 합병정렬, Merge sort)은 퀵 정렬과 마찬가지로 분할 정복을 통해 정렬하는 방식이다. 주어진 배열을 반으로 쪼개는 과정을 반복해서 최대한으로 쪼갠 후, 분할이 끝나면 정렬을 하면서 병합(merge)를 하는 방식이다.
퀵 정렬과 비교해서 병합 정렬의 속도는 대부분의 경우 느리지만, 어떤 경우에도 O(n log n)이라는 일정한 속도를 내고, 안정 정렬이라는 점에서 상용 라이브러리에 많이 사용되고 있다.
병합 정렬 구현하기
병합 정렬은 merge하는 함수와 배열을 쪼개주는 함수 두가지를 이용한다.
def merge(arr1, arr2):
# 결과를 담아줄 빈 배열
result = []
# 하나씩 선택할 포인터
i = j = 0
# 각각 비교 후 result에 담아준다
while i < len (arr1) and j < len(arr2):
if arr1[i] < arr2[j]:
result.append(arr1[i])
i += 1
else:
result.append(arr2[j])
j += 1
# 비교가 끝나고 남은 요소들 result에 삽입
while i < len(arr1):
result.append(arr1[i])
i += 1
while j < len(arr2):
result.append(arr2[j])
j += 1
return result
쪼개준 배열을 정렬해서 다시 합쳐주기 위한 함수이다.
구현하는 방식은 개념을 이해하면 크게 어렵지 않다. while문을 돌리기 때문에 i와 j를 따로 선언해주고, i와 j 포인터가 배열의 끝에 다다를 때까지 반복한다. 배열1과 배열2의 요소 중 더 큰 값을 result 리스트에 넣어주고, 마지막에 남은 요소들을 하나씩 result에 넣어주면 끝이다. 간단하쥬?
def merge_sort(lst):
# 예외 처리
if len(lst) <= 1:
return lst
# 재귀를 이용하여 리스트를 끝까지 쪼개준다.
mid = len(lst) // 2
L = merge_sort(lst[:mid])
R = merge_sort(lst[mid:])
return merge(L, R)
배열을 쪼개주기 위한 함수도 크게 어렵지 않다. 그저 중간 인덱스를 찾아 재귀 호출을 해서 계속 절반씩 쪼개주고, 재귀 구조의 가장 깊숙이까지 들어가서 모든 요소가 쪼개졌다면, 위에서 구현한 merge()함수를 이용해 정렬하고 다시 합쳐주는 과정만 반복해주면 된다.
마치며
평소에도 좋았던건 아니었지만 오늘 유독 공부가 손에 안잡혔다. 다른 때 같았으면 '그래도 해야지...' 하면서 억지로라도 했을 텐데 오늘은 그마저도 싫었다. 밥을 안먹어서 그런가... 오늘은 일찍 자야겠다.

'Study > TIL' 카테고리의 다른 글
| [TIL] 05/30 항해99 22일차 - 동기 & 비동기 (0) | 2022.05.31 |
|---|---|
| [TIL] 05/28 항해99 20일차 - 이진탐색 (0) | 2022.05.28 |
| [TIL] 05/26 항해99 18일차 - 버블/선택/삽입 정렬, 문제풀이 (0) | 2022.05.27 |
| [TIL] 05/25 항해99 17일차 - 힙, 문제풀이 (1) | 2022.05.26 |
| [TIL] 05/24 항해99 16일차 - 이진탐색트리, 문제풀이 (0) | 2022.05.24 |
