
들어가며
쌓인 스트레스 + 컨디션 + 부족한 수면시간 콤보로 하루종일 잠만 잤다.
그 업보로 새벽에 TIL 쓰기 시작하기 형벌을 받게 됐다ㅎ 오늘은 몇시에 잘 수 있을까...
오늘의 TIL은 오늘 배운 트리의 개념과 구현문제를 정리하도록 해보자!
트리
트리란?
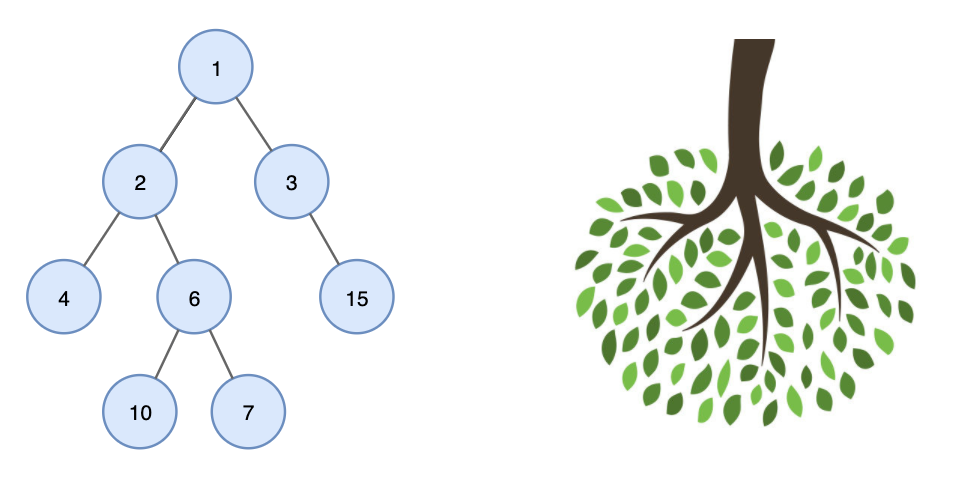
뿌리와 가지로 구성되어 거꾸로 세워놓은 나무처럼 보이는 계층형 비선형 자료구조.
한 가족의 계보를 나타내는 족보나 회사 조직도 같은 것들도 트리 구조 형태로 되어 있다.
트리에서 사용하는 용어
기본적으로 그래프와 크게 다르지 않지만 트리에서 사용하는 용어들을 먼저 알고 들어가보자
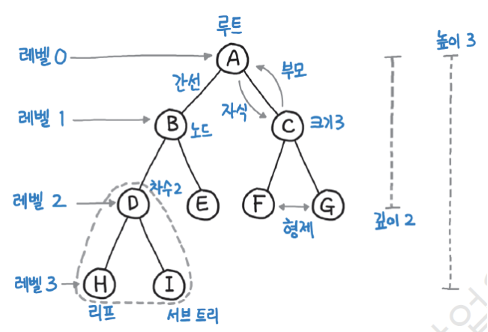
| Node | 트리에서 데이터를 저장하는 기본 요소 |
| Root Node | 트리 맨 위에 있는 노드 |
| Level | 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄 |
| Parent Node | 어떤 노드의 상위 레벨에 연결된 노드 |
| Child Node | 어떤 노드의 하위 레벨에 연결된 노드 |
| Leaf Node | Child Node가 하나도 없는 노드 |
| Sibling | 동일한 Parent Node를 가진 노드 |
| Depth | 트리에서 Node가 가질 수 있는 최대 |
트리의 속성
트리의 속성 중 가장 중요한 것은 ‘루트 노드를 제외한 모든 노드는 단 하나의 부모 노드만을 가진다'는 것이다. 이 속성 때문에 트리는 다음 성질을 만족한다.
- 임의의 노드에서 다른 노드로 가는 경로(path)는 유일하다
- 회로(cycle)가 존재하지 않는다.
- 모든 노드는 서로 연결되어 있다.
- 엣지(edge)를 하나 자르면 트리가 두 개로 분리된다.
- 엣지(edge)의 수는 노드의 수에서 1을 뺀 것과 같다.
트리가 아닌 예시



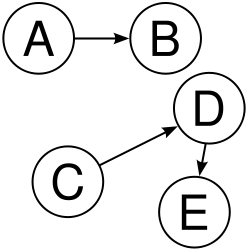
그래프 vs 트리
그래프와 트리는 그림을 보면 비슷하게 생겼다. 이 둘의 차이점은 무엇일까?
가장 큰 차이점은 트리는 순환 구조를 갖지 않는 그래프라는 점이다. 트리는 그래프의 일종이지만, 그래프와 달리 어떠한 경우에도 한번 연결된 노드가 다시 연결되지 않는다.
또, 단방향, 양방향을 모두 가리킬 수 있는 그래프와 달리, 트리는 부모 노드에서 자식 노드를 가리키는 단방향 뿐이다. 그 뿐만 아니라 트리는 단 하나의 부모 노드를 갖는다는 차이점이 있으며, 루트 또한 하나여야한다.
트리의 종류
이진 트리
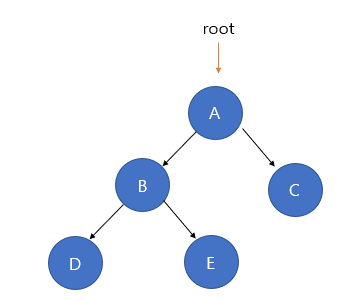
이진 트리(Binary Tree)는 이진 탐색 트리와 함께 트리 중에서 가장 널리 사용되는 트리 자료구조로, 특징은 바로 각 노드가 최대 두 개의 자식을 가진다는 것이다. 즉, 하위의 노드가 0, 1, 2개만 있을 수 있다는 말이다.
완전 이진 트리
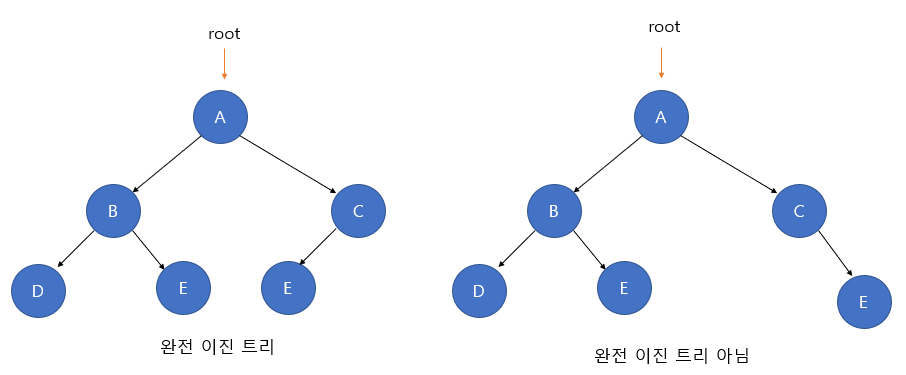
완전 이진 트리(Complete Binary Tree)는 마지막 노드를 제외하고 모든 노드가 완전히 채워져있는 트리 자료구조로, 특징은 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입해야 한다는 것이다.
이진 트리 구현
이진 트리를 만들어보자!
class TreeNode:
def __init__(self, value, left=None, right=None):
self.value = value
self.left = left
self.right = right
def make_tree_by(lst, idx):
parent = None
if idx < len(lst):
value = lst[idx]
if value == None:
return
parent = TreeNode(value)
parent.left = make_tree_by(lst, 2 * idx + 1)
parent.left = make_tree_by(lst, 2 * idx + 2)
return parent
make_tree by(lst, idx) 함수를 살펴보자. 재귀 구조로 구현하는 방식이다.
가장 먼저 parent를 초기화해준다. 다음 조건문을 만족하지 않는다면 parent를 None으로 리턴시켜줘야하기 때문이다.
그리고 나서 index가 list의 길이보다 작은 경우 즉, 내가 이진트리로 만드려는 배열의 길이보다 내가 만드려는 노드의 index가 작을 때 이진트리를 만드는 과정을 진행해주고, 그렇지 않다면 None을 리턴해준다.
value가 None일 때의 종료조건을 만들어준 다음 트리를 하나씩 만들어주는데, 여기서 2 * idx + 1는 뭘까?
간단하게 그림으로 보면 이해가 빠르다.

root 노드인 1의 인덱스는 0이고 2는 1이고... 인덱스를 생각해보자 2의 자식 노드인 4의 인덱스는 3이고, 그 인덱스를 계산하는 방법을 생각해보면 4의 부모노드 2의 인덱스인 1에 2를 곱한 후 1을 더해주면 왼쪽 자식 노드의 인덱스를 구할 수 있다.
위의 모든 과정을 재귀 구조로 마지막까지 실행하면 이진트리가 완성된다.
문제풀이
[leetcode] 104. 이진 트리의 최대 깊이 (Maximum Depth of Binary Tree)
[leetcode] 104. 이진 트리의 최대 깊이 (Maximum Depth of Binary Tree)
들어가며 본 포스팅은 <파이썬 알고리즘 인터뷰> 책에서 다룬 리트코드 문제들을 다루고 있습니다. 문제들은 모두 리트코드에서 출제된 문제들이며, 문제 풀이의 많은 부분을 책의 힌트와 해설
annajin.tistory.com
마치며
항해99의 기술매니저님의 도움을 받아 기초부터 탄탄히 다지기로 했다.
알고리즘을 3주만에 터득하기는 무리가 있으니 나중을 위해서라도 좋은 선택이라는 생각이 든다.
기초부터 시작해서 다시 이진트리 개념까지 공부하러 오는 그날까지 화이팅!
출처
'Study > TIL' 카테고리의 다른 글
| [TIL] 05/25 항해99 17일차 - 힙, 문제풀이 (1) | 2022.05.26 |
|---|---|
| [TIL] 05/24 항해99 16일차 - 이진탐색트리, 문제풀이 (0) | 2022.05.24 |
| [TIL] 05/21 항해99 13일차 - 보안 공격, 백트래킹, 문제풀이 (0) | 2022.05.22 |
| [TIL] 05/20 항해99 12일차 - BFS, DFS vs BFS, 문제풀이 (0) | 2022.05.21 |
| [TIL] 05/19 항해99 11일차 - 그래프, DFS (0) | 2022.05.19 |