
부호/증감 연산자
부호 연산자
| 연산식 | 설명 | |
| + | 피연산자 | 피연산자의 부호 유지 |
| - | 피연산자 | 피연산자의 부호 변경 |
정수 타입(byte, short, int) 연산의 결과는 int 타입이다. 부호를 변경하는 것도 연산이므로 int 타입 변수에 대입해야한다.
증감 연산자
| 연산식 | 설명 | |
| ++ | 피연산자 | 피연산자의 값을 1 증가시킴 |
| -- | 피연산자 | 피연산자의 값을 1 감소시킴 |
| 피연산자 | ++ | 다른 연산을 수행한 후에 피연산자의 값을 1 증가시킴 |
| 피연산자 | -- | 다른 연산을 수행한 후에 피연산자의 값을 1 감소시킴 |
❓for문 증감연산자는 왜 뒤에 ++이 붙을까?
for문의 증감식은 블록 실행 후 루프가 "다시 조건식으로 돌아가기 전에" i값을 증감 시키는 역할을 한다.
즉, 블록 실행 후 i를 증감시켜 다음 루프를 준비하는 것이다...만 for문 증감식에서 후위(i++)과 전위(++i)는 동일하게 동작한다.
산술 연산자
| 연산식 | 설명 | ||
| 피연산자 | + | 피연산자 | 덧셈 연산 |
| 피연산자 | - | 피연산자 | 뺄셈 연산 |
| 피연산자 | * | 피연산자 | 곱셈 연산 |
| 피연산자 | / | 피연산자 | 나눗셈 연산 |
| 피연산자 | % | 피연산자 | 나눗셈의 나머지를 산출하는 연산 |
산술 연산의 특징
- 피연산자가 정수 타입(byte, short, char, int)이면 연산의 결과는 int 타입이다
- 피연산자가 정수 타입이고 그 중 하나가 long 타입이면 연산의 결과는 long 타입이다
- 피연산자 중 하나가 실수 타입이면 연산의 결과는 실수 타입이다
오버플로우와 언더 플로우
오버 플로우: 타입이 허용하는 최대값을 벗어나는 것
언더 플로우: 타입이 허용하는 최소값을 벗어나는 것
오버/언더 플로우가 발생하면 에러가 발생하는 것이 아니라 해당 정수 타입의 최소값 또는 최대값으로 돌아간다.
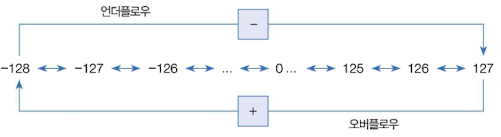
💡연산 과정 중에 발생하는 오버플로우와 언더플로우의 가능성을 미리 예측하고 신경써야한다.
사용하는 타입에서 이 상황이 발생될 가능성이 있다면 범위가 더 큰 타입으로 연산하도록 해야함에 주의하자!
정확한 계산은 정수 연산으로
정확한 계산은 소수점까지 표현되는 실수(double) 타입을 사용해야하는게 아닐까?
정답은 아니다. 정확한 산술 연산이 필요할 때는 정수 타입(int, long)을 쓰는게 권장된다.
왜 정확한 산술 연산은 정수 타입으로 해야 할까?
1. 실수 타입은 근사값을 저장한다.
자바에서 실수(double, float)는 "부동소수점 방식"으로 저장된다.
부동소수점 방식은 메모리 이진수로 근사치를 저장하는 방식을 말한다.
System.out.print(0.1 + 0.2);
// 예상: 0.3 -> 실제 결과: 0.30000000000000004-> 실수 타입은 정확히 0.3을 표현하지 못하고 근사값으로 표현된다.
왜?
실수는 이진수로 정확히 표현할 수 없는 소수점 값이 많다.
부동소수점 방식은 일정 비트수로 수를 표현해야 하기에 반올림 오차(Precision Error)가 발생한다.
2. 정수는 이진수로 정확하게 표현이 가능하다.
덧셈, 뺄셈, 곱셈 등 정수 연산은 오차 없이 정확하게 계산된다.
금액, 개수, 인덱스 등 정확성이 중요한 데이터는 정수로 연산해야 안전하다.
자바에서의 권장사항
- 정확한 값이 필요한 경우 (금융, 수량 등)
-> int, long 사용 - 실제 소수점 값이 필요한 경우 (그래픽, 과학 연산 등)
-> double, float 사용 - 금융처럼 소수점 + 높은 정확성 모두 필요할 때
-> BigDecimal 사용
나눗셈 연산 후 NaN과 Infinity 처리
나눗셈(/) 또는 나머지(%) 연산에서 좌측 피연산자가 정수이고 우측 피연산자가 0일 경우 예외(ArithmeticException)가 발생한다. 무한대의 값을 정소로 표현할 수 없기 때문이다.
int x = 5;
int y = 0;
int result = x / y; // 예외 발생
하지만 좌측 피연산자가 실수이거나 우측 피연산자가 0.0 또는 0.0f이면 예외가 발생하지 않고 연산의 결과는 Infinity(무한대) 또는 NaN(Not a Number)이 된다.
5 / 0.0 -> Infinity
5 % 0.0 -> Nan
따라서, Infinity나 NaN을 확인하는 함수를 사용하는 것이 좋다.
boolean result = Double.isInfinity(변수);
boolean result = Double.isNaN(변수);
비교 연산자
| 구분 | 연산식 | 설명 | ||
| 동등 비교 | 피연산자1 | == | 피연산자2 | 값이 같은지 검사 |
| 피연산자1 | != | 피연산자2 | 값이 다른지 검사 | |
| 크기 비교 | 피연산자1 | > | 피연산자2 | 피연산자1이 큰지 검사 |
| 피연산자1 | >= | 피연산자2 | 피연산자1이 크거나 같은지 검사 | |
| 피연산자1 | < | 피연산자2 | 피연산자1이 작은지 검사 | |
| 피연산자1 | <= | 피연산자2 | 피연산자1이 작거나 같은지 검사 | |
예외
float 동등 비교
0.1f == 0.1 -> false
부동 소수점 방식을 사용하는 실수 타입은 0.1을 정확히 표현할 수 없을 뿐만 아니라 float 타입과 double 타입의 정밀도 타입 때문에 다음과 같은 현상이 발생한다.
이런 경우 피연산자를 float 타입으로 강제 타입 변환 후 비교 연산을 수행한다.
문자열 비교
문자열 비교는 다음 함수를 사용한다.
boolean result = str1.equals(str2); // 대소문자 구분
boolean result = !str1.equals(str2);
논리 연산자
| 구분 | 연산식 | 결과 | 설명 | ||
| AND(논리곱) | true | && 또는 & | true | true | 피연산자 모두가 true일 경우에만 연산 결과가 true |
| true | false | false | |||
| false | false | false | |||
| false | false | false | |||
| OR(논리합) | true | || 또는 | | true | true | 피연산자 중 하나만 true이면 연산 결과는 true |
| true | false | true | |||
| false | true | true | |||
| false | false | false | |||
| XOR(베타적 논리합) | true | ^ | true | false | 피연산자 중 하나는 true이고 다른 하나가 false일 경우에만 연산 결과가 true |
| true | false | true | |||
| false | true | true | |||
| false | false | false | |||
| NOT(논리 부정) | ! | true | false | 피연산자의 논리값을 바꿈 | |
| false | true | ||||
&& vs & (|| vs |)
&&와 &는 산출 결과는 같지만 연산 과정이 조금 다르다.
&& (||)
앞의 피연산자가 false이면 뒤의 피연산자를 평가하지 않고 바로 false를 산출한다 (Short-circuit)
불필요한 연산을 줄여 성능을 향상시키고 NPE 같은 예외를 방지할 수 있다.
if (obj != null && obj.lenght() > 0) {
// obj가 null이면 obj.length()는 실행하지 않음
}
&(|)
두 피연산자를 모두 평가해서 산출 결과를 낸다.
비트 연산이 필요하거나 모든 조건을 반드시 체크해야 할 때 사용한다.
비트 논리 연산자
비트 논리 연산자는 bit 단위로 논리 연산을 수행한다. 0과 1이 피연산자가 되므로 정수 타입만 피연산자가 될 수 있다.
1은 true, 0은 false라는 점을 제외하고는 논리 연산자와 동일하다
| 구분 | 연산식 | 결과 | 설명 | ||
| AND(논리곱) | 1 | & | 1 | 1 | 두 비트 모두가 1일 경우에만 연산 결과가 1 |
| 1 | 0 | 0 | |||
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | |||
| OR(논리합) | 1 | | | 1 | 1 | 두 비트 중 하나만 1이면 연산 결과는 1 |
| 1 | 0 | 1 | |||
| 0 | 1 | 1 | |||
| 0 | 0 | 0 | |||
| XOR(베타적 논리합) | 1 | ^ | 1 | 0 | 두 비트 중 하나는 1이고 다른 하나가 0일 경우에만 연산 결과가 1 |
| 1 | 0 | 1 | |||
| 0 | 1 | 1 | |||
| 0 | 0 | 0 | |||
| NOT(논리 부정) | ~ | 1 | 0 | 보수 | |
| 0 | 1 | ||||
비트 이동 연산자
비트 이동 연산자는 비트를 좌측 또는 우측으로 빌어서 이동시키는 연산을 수행한다
| 구분 | 연산식 | 설명 | ||
| 이동(shift) | a | << | b | 정수 a의 각 비트를 b만큼 왼쪽으로 이동 오른쪽 빈자리는 0으로 채움 a x 2^b와 동일한 결과가 됨 |
| a | >> | b | 정수 a의 각 비트를 b만큼 오른쪽으로 이동 왼쪽 빈자리는 최상위 부호 비트와 같은 값으로 채움 a / 2^b와 동일한 결과가 됨 |
|
| a | >>> | b | 정수 a의 각 비트를 b만큼 오른쪽으로 이동 왼쪽 빈자리는 0으로 채움 |
|
대입 연산자
| 구분 | 연산식 | 설명 | ||
| 단순 대입 연산자 | 변수 | = | 피연산자 | 우측의 피연산자의 값을 변수에 저장 |
| 변수 | += | 피연산자 | 우측의 피연산자의 값을 변수의 값과 더한 후에 다시 변수에 저장 (변수 = 변수 + 피연산자) | |
| 변수 | -= | 피연산자 | 우측의 피연산자의 값을 변수의 값에서 뺀 후에 다시 변수에 저장 (변수 = 변수 - 피연산자) | |
| 변수 | *= | 피연산자 | 우측의 피연산자의 값을 변수의 값과 곱한 후에 다시 변수에 저장 (변수 = 변수 * 피연산자) | |
| 변수 | /= | 피연산자 | 우측의 피연산자의 값으로 변수의 값을 나눈 후에 다시 변수에 저장 (변수 = 변수 / 피연산자) | |
| 변수 | %= | 피연산자 | 우측의 피연산자의 값으로 변수의 값을 나눈 후에 나머지를 변수에 저장 (변수 = 변수 % 피연산자) | |
| 복합 대입 연산자 | 변수 | &= | 피연산자 | 우측의 피연산자의 값과 변수의 값을 & 연산 후 결과를 변수에 저장 (변수 = 변수 & 피연산자) |
| 변수 | |= | 피연산자 | 우측의 피연산자의 값과 변수의 값을 | 연산 후 결과를 변수에 저장 (변수 = 변수 | 피연산자) | |
| 변수 | ^= | 피연산자 | 우측의 피연산자의 값과 변수의 값을 ^ 연산 후 결과를 변수에 저장 (변수 = 변수 ^ 피연산자) | |
| 변수 | <<= | 피연산자 | 우측의 피연산자의 값만큼 변수의 값을 <<연산 후 결과를 변수에 저장 (변수 = 변수 << 피연산자) | |
| 변수 | >>= | 피연산자 | 우측의 피연산자의 값만큼 변수의 값을 >> 연산 후 결과를 변수에 저장 (변수 = 변수 >> 피연산자) | |
| 변수 | >>>= | 피연산자 | 우측의 피연산자의 값만큼 변수의 값을 >>> 연산 후 결과를 변수에 저장 (변수 = 변수 >>> 피연산자) | |
삼항(조건) 연산자
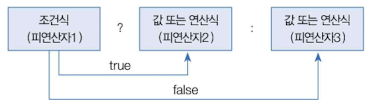
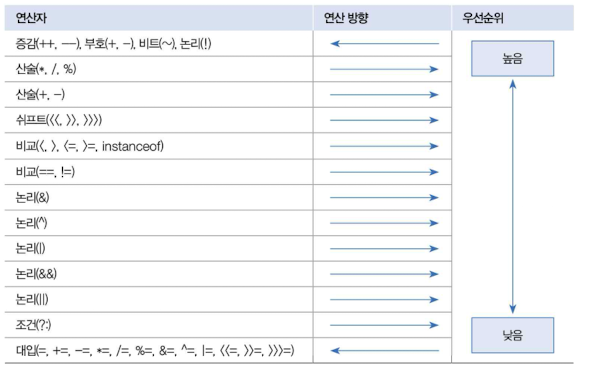
연산의 방향과 우선순위
논리 연산자보다 비교 연산자가 우선순위가 높다.
우선순위가 같은 경우 왼쪽에서 오른쪽으로 연산을 수행한다.
우선순위는 수학에서처럼 괄호()가 우선이다. 그래서 먼저 처리해야 할 연산을 괄호()로 묶는 것을 추천한다고
확인문제
1번 정답: 31
--연산자는 연산이 끝난 후 실행되기 때문에 11 + 20 = 30이 된다.
2번 정답: "가"
score>90 -> false
!(score>90) -> true
3번 정답:
int pencilsPerStudent = penclis / students; // 학생 한 명이 가지는 연필 수
int pnecilsLeft = pencils % students; // 남은 연필 수
4번 정답:
(value / 100) * 100
5번 정답: 1, 2, 3, 4
6번 정답:
true && true -> true
false || false -> false
7번 정답:
Double.isNaN(y)'JAVA > 이것이 자바다' 카테고리의 다른 글
| [이것이 자바다] CH04. 조건문과 반복문, 확인문제 (1) | 2025.03.17 |
|---|---|
| [이것이 자바다] CH02. 변수와 타입, 확인문제 (0) | 2025.03.16 |
| [이것이 자바다] CH01. 자바 시작하기, 확인문제 (3) | 2025.03.16 |

부호/증감 연산자
부호 연산자
| 연산식 | 설명 | |
| + | 피연산자 | 피연산자의 부호 유지 |
| - | 피연산자 | 피연산자의 부호 변경 |
정수 타입(byte, short, int) 연산의 결과는 int 타입이다. 부호를 변경하는 것도 연산이므로 int 타입 변수에 대입해야한다.
증감 연산자
| 연산식 | 설명 | |
| ++ | 피연산자 | 피연산자의 값을 1 증가시킴 |
| -- | 피연산자 | 피연산자의 값을 1 감소시킴 |
| 피연산자 | ++ | 다른 연산을 수행한 후에 피연산자의 값을 1 증가시킴 |
| 피연산자 | -- | 다른 연산을 수행한 후에 피연산자의 값을 1 감소시킴 |
❓for문 증감연산자는 왜 뒤에 ++이 붙을까?
for문의 증감식은 블록 실행 후 루프가 "다시 조건식으로 돌아가기 전에" i값을 증감 시키는 역할을 한다.
즉, 블록 실행 후 i를 증감시켜 다음 루프를 준비하는 것이다...만 for문 증감식에서 후위(i++)과 전위(++i)는 동일하게 동작한다.
산술 연산자
| 연산식 | 설명 | ||
| 피연산자 | + | 피연산자 | 덧셈 연산 |
| 피연산자 | - | 피연산자 | 뺄셈 연산 |
| 피연산자 | * | 피연산자 | 곱셈 연산 |
| 피연산자 | / | 피연산자 | 나눗셈 연산 |
| 피연산자 | % | 피연산자 | 나눗셈의 나머지를 산출하는 연산 |
산술 연산의 특징
- 피연산자가 정수 타입(byte, short, char, int)이면 연산의 결과는 int 타입이다
- 피연산자가 정수 타입이고 그 중 하나가 long 타입이면 연산의 결과는 long 타입이다
- 피연산자 중 하나가 실수 타입이면 연산의 결과는 실수 타입이다
오버플로우와 언더 플로우
오버 플로우: 타입이 허용하는 최대값을 벗어나는 것
언더 플로우: 타입이 허용하는 최소값을 벗어나는 것
오버/언더 플로우가 발생하면 에러가 발생하는 것이 아니라 해당 정수 타입의 최소값 또는 최대값으로 돌아간다.

💡연산 과정 중에 발생하는 오버플로우와 언더플로우의 가능성을 미리 예측하고 신경써야한다.
사용하는 타입에서 이 상황이 발생될 가능성이 있다면 범위가 더 큰 타입으로 연산하도록 해야함에 주의하자!
정확한 계산은 정수 연산으로
정확한 계산은 소수점까지 표현되는 실수(double) 타입을 사용해야하는게 아닐까?
정답은 아니다. 정확한 산술 연산이 필요할 때는 정수 타입(int, long)을 쓰는게 권장된다.
왜 정확한 산술 연산은 정수 타입으로 해야 할까?
1. 실수 타입은 근사값을 저장한다.
자바에서 실수(double, float)는 "부동소수점 방식"으로 저장된다.
부동소수점 방식은 메모리 이진수로 근사치를 저장하는 방식을 말한다.
System.out.print(0.1 + 0.2);
// 예상: 0.3 -> 실제 결과: 0.30000000000000004-> 실수 타입은 정확히 0.3을 표현하지 못하고 근사값으로 표현된다.
왜?
실수는 이진수로 정확히 표현할 수 없는 소수점 값이 많다.
부동소수점 방식은 일정 비트수로 수를 표현해야 하기에 반올림 오차(Precision Error)가 발생한다.
2. 정수는 이진수로 정확하게 표현이 가능하다.
덧셈, 뺄셈, 곱셈 등 정수 연산은 오차 없이 정확하게 계산된다.
금액, 개수, 인덱스 등 정확성이 중요한 데이터는 정수로 연산해야 안전하다.
자바에서의 권장사항
- 정확한 값이 필요한 경우 (금융, 수량 등)
-> int, long 사용 - 실제 소수점 값이 필요한 경우 (그래픽, 과학 연산 등)
-> double, float 사용 - 금융처럼 소수점 + 높은 정확성 모두 필요할 때
-> BigDecimal 사용
나눗셈 연산 후 NaN과 Infinity 처리
나눗셈(/) 또는 나머지(%) 연산에서 좌측 피연산자가 정수이고 우측 피연산자가 0일 경우 예외(ArithmeticException)가 발생한다. 무한대의 값을 정소로 표현할 수 없기 때문이다.
int x = 5;
int y = 0;
int result = x / y; // 예외 발생
하지만 좌측 피연산자가 실수이거나 우측 피연산자가 0.0 또는 0.0f이면 예외가 발생하지 않고 연산의 결과는 Infinity(무한대) 또는 NaN(Not a Number)이 된다.
5 / 0.0 -> Infinity
5 % 0.0 -> Nan
따라서, Infinity나 NaN을 확인하는 함수를 사용하는 것이 좋다.
boolean result = Double.isInfinity(변수);
boolean result = Double.isNaN(변수);
비교 연산자
| 구분 | 연산식 | 설명 | ||
| 동등 비교 | 피연산자1 | == | 피연산자2 | 값이 같은지 검사 |
| 피연산자1 | != | 피연산자2 | 값이 다른지 검사 | |
| 크기 비교 | 피연산자1 | > | 피연산자2 | 피연산자1이 큰지 검사 |
| 피연산자1 | >= | 피연산자2 | 피연산자1이 크거나 같은지 검사 | |
| 피연산자1 | < | 피연산자2 | 피연산자1이 작은지 검사 | |
| 피연산자1 | <= | 피연산자2 | 피연산자1이 작거나 같은지 검사 | |
예외
float 동등 비교
0.1f == 0.1 -> false
부동 소수점 방식을 사용하는 실수 타입은 0.1을 정확히 표현할 수 없을 뿐만 아니라 float 타입과 double 타입의 정밀도 타입 때문에 다음과 같은 현상이 발생한다.
이런 경우 피연산자를 float 타입으로 강제 타입 변환 후 비교 연산을 수행한다.
문자열 비교
문자열 비교는 다음 함수를 사용한다.
boolean result = str1.equals(str2); // 대소문자 구분
boolean result = !str1.equals(str2);
논리 연산자
| 구분 | 연산식 | 결과 | 설명 | ||
| AND(논리곱) | true | && 또는 & | true | true | 피연산자 모두가 true일 경우에만 연산 결과가 true |
| true | false | false | |||
| false | false | false | |||
| false | false | false | |||
| OR(논리합) | true | || 또는 | | true | true | 피연산자 중 하나만 true이면 연산 결과는 true |
| true | false | true | |||
| false | true | true | |||
| false | false | false | |||
| XOR(베타적 논리합) | true | ^ | true | false | 피연산자 중 하나는 true이고 다른 하나가 false일 경우에만 연산 결과가 true |
| true | false | true | |||
| false | true | true | |||
| false | false | false | |||
| NOT(논리 부정) | ! | true | false | 피연산자의 논리값을 바꿈 | |
| false | true | ||||
&& vs & (|| vs |)
&&와 &는 산출 결과는 같지만 연산 과정이 조금 다르다.
&& (||)
앞의 피연산자가 false이면 뒤의 피연산자를 평가하지 않고 바로 false를 산출한다 (Short-circuit)
불필요한 연산을 줄여 성능을 향상시키고 NPE 같은 예외를 방지할 수 있다.
if (obj != null && obj.lenght() > 0) {
// obj가 null이면 obj.length()는 실행하지 않음
}
&(|)
두 피연산자를 모두 평가해서 산출 결과를 낸다.
비트 연산이 필요하거나 모든 조건을 반드시 체크해야 할 때 사용한다.
비트 논리 연산자
비트 논리 연산자는 bit 단위로 논리 연산을 수행한다. 0과 1이 피연산자가 되므로 정수 타입만 피연산자가 될 수 있다.
1은 true, 0은 false라는 점을 제외하고는 논리 연산자와 동일하다
| 구분 | 연산식 | 결과 | 설명 | ||
| AND(논리곱) | 1 | & | 1 | 1 | 두 비트 모두가 1일 경우에만 연산 결과가 1 |
| 1 | 0 | 0 | |||
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | |||
| OR(논리합) | 1 | | | 1 | 1 | 두 비트 중 하나만 1이면 연산 결과는 1 |
| 1 | 0 | 1 | |||
| 0 | 1 | 1 | |||
| 0 | 0 | 0 | |||
| XOR(베타적 논리합) | 1 | ^ | 1 | 0 | 두 비트 중 하나는 1이고 다른 하나가 0일 경우에만 연산 결과가 1 |
| 1 | 0 | 1 | |||
| 0 | 1 | 1 | |||
| 0 | 0 | 0 | |||
| NOT(논리 부정) | ~ | 1 | 0 | 보수 | |
| 0 | 1 | ||||
비트 이동 연산자
비트 이동 연산자는 비트를 좌측 또는 우측으로 빌어서 이동시키는 연산을 수행한다
| 구분 | 연산식 | 설명 | ||
| 이동(shift) | a | << | b | 정수 a의 각 비트를 b만큼 왼쪽으로 이동 오른쪽 빈자리는 0으로 채움 a x 2^b와 동일한 결과가 됨 |
| a | >> | b | 정수 a의 각 비트를 b만큼 오른쪽으로 이동 왼쪽 빈자리는 최상위 부호 비트와 같은 값으로 채움 a / 2^b와 동일한 결과가 됨 |
|
| a | >>> | b | 정수 a의 각 비트를 b만큼 오른쪽으로 이동 왼쪽 빈자리는 0으로 채움 |
|
대입 연산자
| 구분 | 연산식 | 설명 | ||
| 단순 대입 연산자 | 변수 | = | 피연산자 | 우측의 피연산자의 값을 변수에 저장 |
| 변수 | += | 피연산자 | 우측의 피연산자의 값을 변수의 값과 더한 후에 다시 변수에 저장 (변수 = 변수 + 피연산자) | |
| 변수 | -= | 피연산자 | 우측의 피연산자의 값을 변수의 값에서 뺀 후에 다시 변수에 저장 (변수 = 변수 - 피연산자) | |
| 변수 | *= | 피연산자 | 우측의 피연산자의 값을 변수의 값과 곱한 후에 다시 변수에 저장 (변수 = 변수 * 피연산자) | |
| 변수 | /= | 피연산자 | 우측의 피연산자의 값으로 변수의 값을 나눈 후에 다시 변수에 저장 (변수 = 변수 / 피연산자) | |
| 변수 | %= | 피연산자 | 우측의 피연산자의 값으로 변수의 값을 나눈 후에 나머지를 변수에 저장 (변수 = 변수 % 피연산자) | |
| 복합 대입 연산자 | 변수 | &= | 피연산자 | 우측의 피연산자의 값과 변수의 값을 & 연산 후 결과를 변수에 저장 (변수 = 변수 & 피연산자) |
| 변수 | |= | 피연산자 | 우측의 피연산자의 값과 변수의 값을 | 연산 후 결과를 변수에 저장 (변수 = 변수 | 피연산자) | |
| 변수 | ^= | 피연산자 | 우측의 피연산자의 값과 변수의 값을 ^ 연산 후 결과를 변수에 저장 (변수 = 변수 ^ 피연산자) | |
| 변수 | <<= | 피연산자 | 우측의 피연산자의 값만큼 변수의 값을 <<연산 후 결과를 변수에 저장 (변수 = 변수 << 피연산자) | |
| 변수 | >>= | 피연산자 | 우측의 피연산자의 값만큼 변수의 값을 >> 연산 후 결과를 변수에 저장 (변수 = 변수 >> 피연산자) | |
| 변수 | >>>= | 피연산자 | 우측의 피연산자의 값만큼 변수의 값을 >>> 연산 후 결과를 변수에 저장 (변수 = 변수 >>> 피연산자) | |
삼항(조건) 연산자

연산의 방향과 우선순위
논리 연산자보다 비교 연산자가 우선순위가 높다.
우선순위가 같은 경우 왼쪽에서 오른쪽으로 연산을 수행한다.
우선순위는 수학에서처럼 괄호()가 우선이다. 그래서 먼저 처리해야 할 연산을 괄호()로 묶는 것을 추천한다고

확인문제
1번 정답: 31
--연산자는 연산이 끝난 후 실행되기 때문에 11 + 20 = 30이 된다.
2번 정답: "가"
score>90 -> false
!(score>90) -> true
3번 정답:
int pencilsPerStudent = penclis / students; // 학생 한 명이 가지는 연필 수
int pnecilsLeft = pencils % students; // 남은 연필 수
4번 정답:
(value / 100) * 100
5번 정답: 1, 2, 3, 4
6번 정답:
true && true -> true
false || false -> false
7번 정답:
Double.isNaN(y)'JAVA > 이것이 자바다' 카테고리의 다른 글
| [이것이 자바다] CH04. 조건문과 반복문, 확인문제 (1) | 2025.03.17 |
|---|---|
| [이것이 자바다] CH02. 변수와 타입, 확인문제 (0) | 2025.03.16 |
| [이것이 자바다] CH01. 자바 시작하기, 확인문제 (3) | 2025.03.16 |
