
들어가며
알고리즘 1주차가 끝나는 날이다. 항해99 알고리즘 주차에서는 한 주차가 끝날 때마다 테스트를 보게되고, 오늘 그 테스트를 보았다. 사실 1주차 내내 개념 정리에 주로 힘을 써왔기 때문에 구현에는 자신이 없어서 테스트를 잘 볼 수 있을까 걱정했는데 아니나 다를까 어렵더라… 어찌저찌해서 결국 해결은 했는데 문제를 풀어냈다!라는 기쁨보다는 여전히 한참 부족하다는 자괴감이 많이 들었다. 테스트 2시간이었는데 시간이 부족해서 추가시간까지 쓰고 나서야 겨우 해결을 하는 바람에 오늘 문제공부를 할 시간이 부족했다.
…라고 오늘 문제풀이를 못하는 이유를 늘어놨는데 결론은 오늘의 TIL은 항해99의 커리큘럼에 따라 그래프와 DFS의 간단한 개념을 정리해보고자한다!
그래프
그래프는 정점(vertex)와 간선(edge)으로 구성된 한정된 자료구조를 의미한다.
출처 - 위키백과
정점과 간선은 비전공자인 나에게 익숙한 들어본 단어는 아니다. 쉽게 말하자면 정점(vertex)는 각각의 노드(Node)를 말하고, 간선(edge)는 각 노드를 연결하고, 노드 간의 관계를 표시한 선이며, 그래프는 각 정점 간의 관계를 표현하는 조직도라고 볼 수 있다.
자료구조로서의 그래프는 수학자 오일러(Euler)에 의해 창안되어 오랜 기간 연구되어왔지만, 컴퓨터 과학 분야에서 그래프 알고리즘을 다루기 시작한 건 오래되지 않았다고 한다. 그래서 아직 더 쉽게 연구되지 않았고, 공부하는 사람들에게 고통을 안겨주고있다.
본격적인 그래프의 개념으로 들어가기 전에 오일러가 그래프를 창안하게 된 오일러 경로에 대해 간단하게만 알아보고 시작하자.

오일러 경로
우리가 종종 해봤던 한붓그리기가 바로 오일러 경로이다. 아주 옛날에 쾨니히스베르크에 흐르던 프레겔 강에는 2개의 큰 섬이 있었고 섬과 도시를 연결하는 7개의 다리가 놓여있었는데, 어느날 시민 한명이 “이 7개 다리를 한 번씩만 건너서 모두 지나갈 수 있을까?”라는 문제를 냈다고 한다.
모두가 쉽게 풀릴거라고 예상했던 것과 달리 이 문제를 풀 수 있는 이는 아무도 없었다.
이 문제를 연구하던 사람 중 한명이 바로 ‘수학의 모차르트'라고 불리는 레온하르트 오일러였다.
오일러는 이 문제가 도형 문제처럼 보이지만 당시까지 알려진 기하학으로는 풀수 없음을 알았고, 미지의 영역에 그 해법이 있다는 사실을 간파한 것이 ‘그래프 이론’의 시작이라고 한다.
오일러 경로 이외에도 해밀턴 경로, 외판원 문제등 그래프와 관련된 알고리즘 문제들이 존재하니 궁금하다면 구글에게 물어보는걸로 하고, 다시 그래프의 개념으로 넘어가보자.
그래프에서 사용하는 용어
어려운 개념이니 만큼 용어를 알지 못하면 두배로 어려워질테니 용어부터 알고 가자.
| 정점(vertice) | 노드(node)라고도 하며 정점에는 데이터가 저장된다. |
| 간선(edge) | 링크(link)라고도 하며 노드간의 관계를 나타냅니다. |
| 인접 정점(adjacent vertex) | 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점을 뜻한다. |
| 단순 경로(simple-path) | 경로 중 반복되는 정점이 없는것. 같은 간선을 자나가지 않는 경로. |
| 차수(degree) | 정점에 연결된 간선의 수를 말한다. |
| 진출 차수(out-degree) | 방향그래프에서 사용되는 용어로 한 노드에서 외부로 향하는 간선의 수를 뜻한다. |
| 진입차수(in-degree) | 방향그래프에서 사용되는 용어로 외부 노드에서 들어오는 간선의 수를 뜻한다. |
대표적인 그래프의 종류
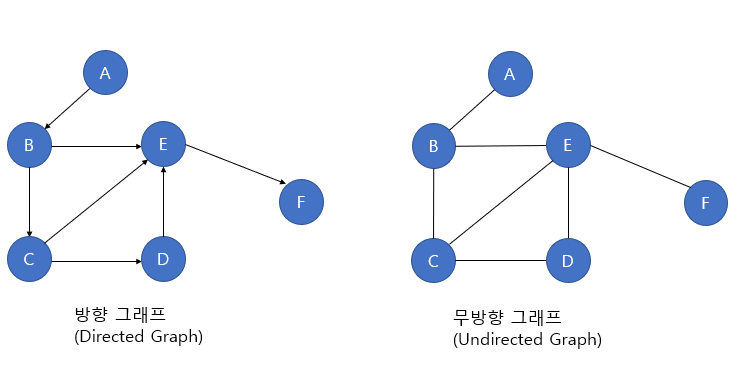
무방향 그래프 (Undirected Graph)
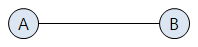
두 정점을 연결하는 간선에 방향이 없는 그래프. 양방향으로 이동이 가능하다.
방향 그래프 (Directed Graph)
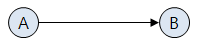
두 정점을 연결하는 간선에 방향이 존재하는 그래프. 간선의 방향으로만 이동이 가능하다.
가중치 그래프 (Weighted Graph)
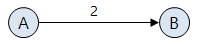
간선에 비용(cost) 또는 가중치(weight)가 할당된 그래프. 두 정점을 이동할 때 비용이 드는 그래프로, 네트워크(network)라고도 불린다.
완전 그래프 (Complete Graph)
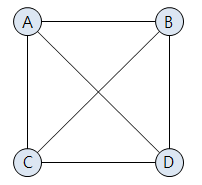
모든 정점 간에 간선이 존재하는 그래프.
그래프의 구현 방법
그래프의 구현 방법에는 배열을 사용하는 인접 행렬(Adjacency Matrix)과 연결리스트를 사용하는 인접 리스트(Adjacency List)가 있다.
인접 행렬 (Adjacency Matrix)
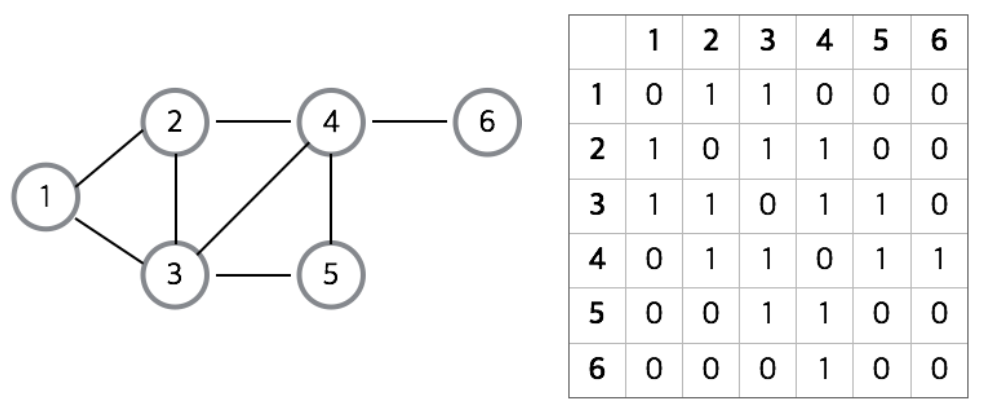
인접 행렬은 2차원 배열로 그래프의 노드간 연결 관계를 표현한 것이다.
그림처럼 1 2 3 4 5 6 각각의 정점과 인접해있는 정점은 1, 인접하지 않은 정점은 0을 넣어준다. 참고로 자기 자신으로 연결되는 간선이 없으므로 배열의 대각선은 모두 0이다.
이를 배열로 표현하면 다음과 같다.
graph = [
[False, True, False, False],
[True, False, True, False],
[False, True, False, True],
[False, False, True, False]
]
장점
- 2차원 배열에 모든 저점들의 간선 정보가 있기 때문에, 두 정점을 연결하는 간선을 조회할 때
O(1)시간 복잡도로 가능하다. - 정점의 차수를 구할 때는 인접행렬의 i번째 행의 값을 모두 더하면 되므로
O(n)의 시간 복잡도로 가능하다. - 구현이 비교적 간단하다.
단점
- 간선의 개수와 무관하게 항상 n^2 크기의 2차원 배열이 필요하므로 메모리 공간이 낭비된다.
- 그래프의 모든 차수를 알아내려면 인접행렬 전체를 확인해야 하므로
O(n^2)의 시간이 소요된다.
인접 리스트 (Adjacency List)
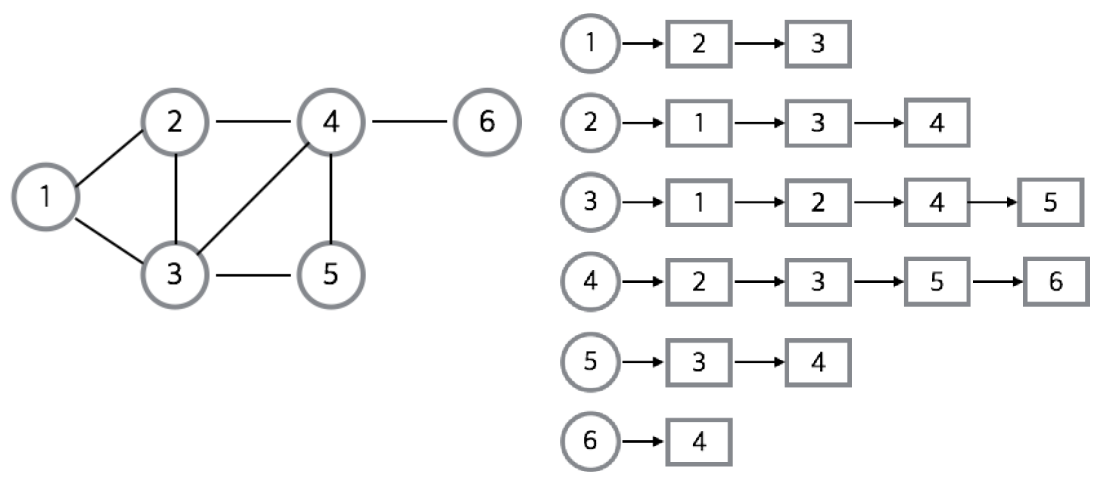
인접 리스트는 각 정점에 인접한 정점들을 연결 리스트로 표현한 것이다. 그림은 무방향 그래프를 나타낸 것인데, 무방향 그래프의 경우에는 각 정점에 연결된 모든 정점을 저장한다.
이를 딕셔너리로 표현하면 다음과 같다.
graph = {
0: [1],
1: [0, 2]
2: [1, 3]
3: [2]
}
장점
- 정점들의 연결 정보를 탐색할 때
O(n)의 시간 복잡도로 가능하다. - 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.
단점
- 두 정점을 연결하는 간선을 조회하거나 정점의 차수를 알기 위해서는 정점의 인접 리스트를 탐색해야 하므로 인접 행렬에 비해 시간이 오래 걸린다.
- 구현이 비교적 어렵다.
인접 행렬 vs 인접 리스트
인접 행렬과 인접 리스트의 차이를 간단하게 정리하자면
인접 행렬은 시간이 빠르지만 공간이 낭비되고, 인접 리스트는 공간의 낭비가 적지만 시간이 비교적 느리다.
그래프 탐색 (순회)
깊이 우선 탐색 (DFS, Depth First Search)
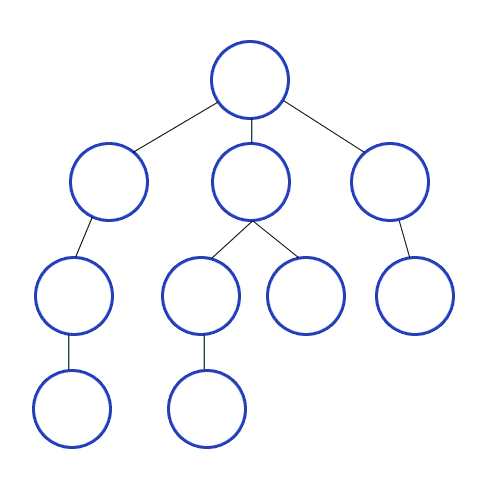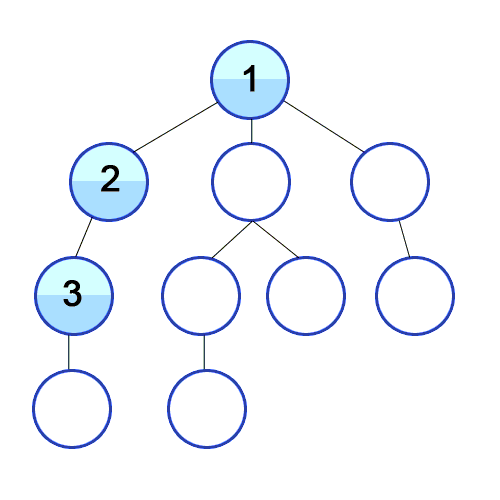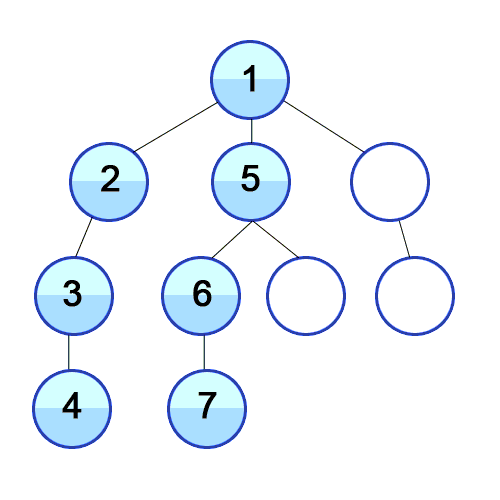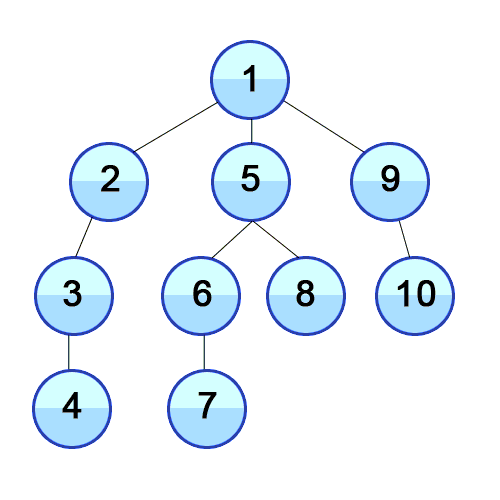
DFS는 특정 노드에서 시작해 다음 분기로 넘어가기 전에 해당 분기를 완전히 탐색하는 방법이다.
쉽게 말하면, 갈 수 있는 만큼 최대한 깊이 가고 더 이상 갈 곳이 없다면 이전 정점으로 돌아가는 방식으로 그래프를 순회하는 방식이다.
DFS는 일반적으로 스택으로 구현하기는 하지만 재귀를 이용하면 조금 더 간단하게 구현할 수 있어서 코딩 테스트 시에 재귀 구현이 더 선호되는 편이라고 한다.
DFS를 예시를 들어가며 자세하게 설명해주는 글이 있어 첨부한다.
[알고리즘] 깊이 우선 탐색, DFS(Depth First Search)알고리즘이란?
DFS 구현하기
재귀 구조로 구현한 코드
DFS를 재귀를 이용하여 구현한 구체적인 동작 과정은 다음과 같다.
- 탐색 시작 노드를 스택에 삽입하고 방문처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접노드가 있으면 다시 함수를 재귀 호출한다
- 종료가 되면 방문한 노드를 순서대로 리턴한다.
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
def dfs_recursive(node, visited):
# 방문처리
visited.append(node)
# 인접 노드 방문
for adj in graph[node]:
if adj not in visited:
dfs_recursive(adj, visited)
return visited
assert dfs_recursive(1, []) == [1, 2, 5, 6, 7, 3, 4]
위 코드의 흐름을 그림으로 나타내면 다음과 같다.
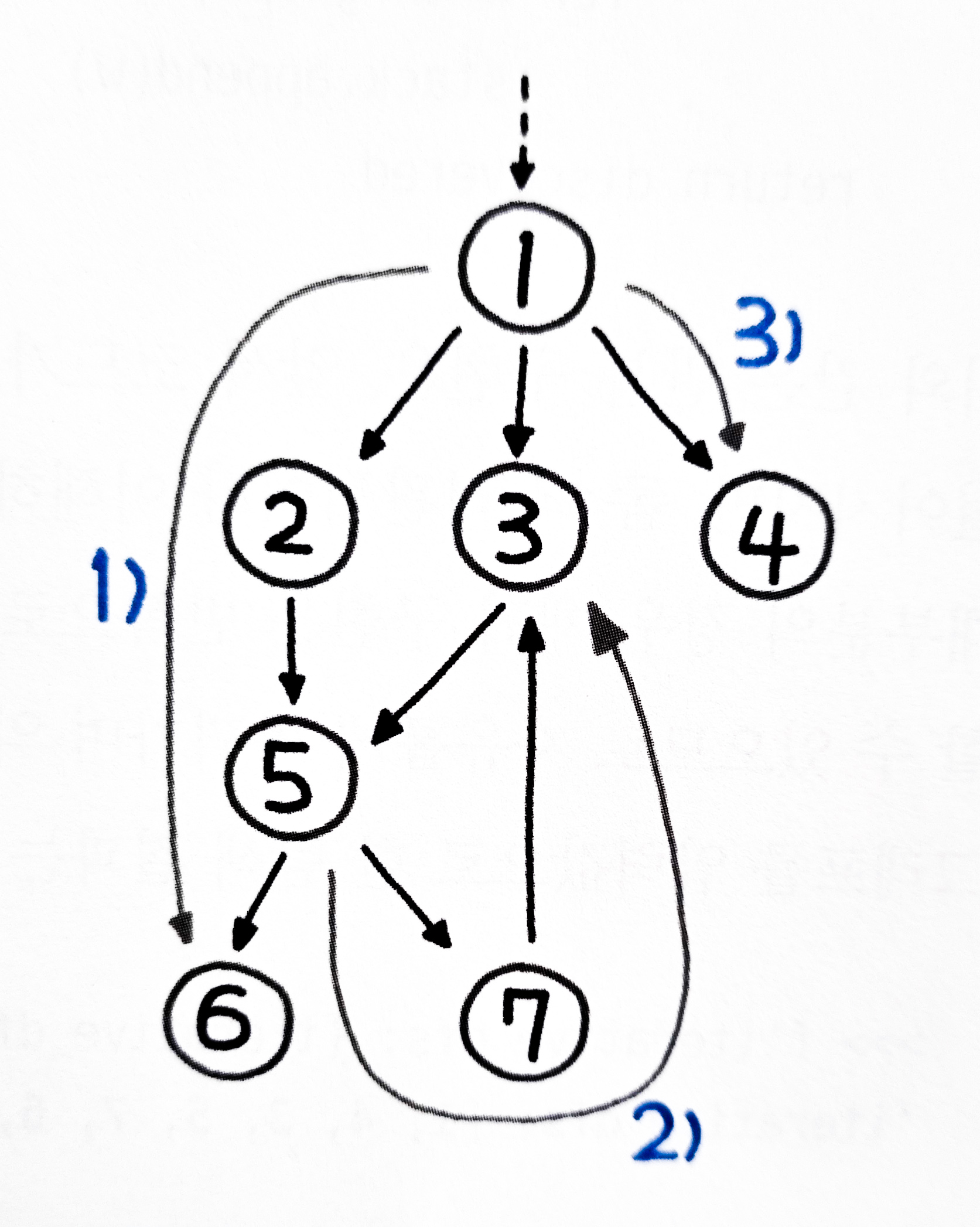
재귀 구조는 포스팅을 쓸 때마다 느끼는 거지만 글로 설명하기가 되게 어렵다. 사실 글로 표현을 한다 하더라도 이해하기가 그닥 쉽지는 않다.
고민하던 차에 항해99 과제톡에서 다른 수강생분이 아주 유용한 웹사이트를 알려주셨기에 기록 겸 링크를 걸어두겠다.
https://pythontutor.com/visualize.html#mode=edit
Python Tutor - Visualize Python, Java, JavaScript, C, C++, Ruby code execution
Write code in Python 3.6 Java 8 JavaScript ES6 C (gcc 9.3, C17 + GNU extensions) C++ (g++ 9.3, C++20 + GNU extensions) ------ [unsupported] Python 2.7 [unsupported] C (gcc 4.8, C11) [unsupported] C++ (g++ 4.8, C++11) [unsupported] TypeScript 1.4 [unsupport
pythontutor.com
코드를 넣으면 그 코드를 그림으로 한줄한줄 표현해주는 사이트인데 코드의 흐름을 이해하기에 매우 도움이 된다.
재귀 구조의 경우 코드만 보고서는 이해하기가 힘들기 때문에 그림으로 보면 이해가 쏙쏙 되는데 이렇게 코드 한줄한줄을 직관적으로 보여주니 너무 좋다. 웹사이트 이름이 <파이썬 튜터>이지만 JAVA, JS, C, C++ 모두 선택 가능하니 사용해보는 걸 추천한다!
스택을 이용한 반복 구조로 구현한 코드
스택을 이용한 DFS의 구체적인 동작 과정은 다음과 같다
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
def dfs_stack(start):
visited = []
# 방문할 순서를 담아두는 용도
stack = [start]
# 방문할 노드가 남아있는 한 아래 로직을 반복한다.
while stack:
# 제일 최근에 삽입된 노드를 꺼내고 방문처리한다.
top = stack.pop()
visited.append(top)
# 인접 노드를 방문한다.
for adj in graph[top]:
if adj not in visited:
stack.append(adj)
return visited
assert dfs_stack(1) == [1, 4, 3, 5, 7, 6, 2]
마치며
과제를 풀지 못한 상태에서 과제톡을 들었는데, 설명을 들으면서 책을 봤을 때 코드가 이해하기가 어려웠다.
DFS가 되게 어려운 알고리즘이라고 많은 분들이 말하시는데 과제톡을 통해서 확실히 깨달았다. 앞으로 더 어려운 개념들이 나올텐데 많은 공부가 필요할 것 같다.
출처
https://suyeon96.tistory.com/32
https://coding-factory.tistory.com/610
'Study > TIL' 카테고리의 다른 글
| [TIL] 05/21 항해99 13일차 - 보안 공격, 백트래킹, 문제풀이 (0) | 2022.05.22 |
|---|---|
| [TIL] 05/20 항해99 12일차 - BFS, DFS vs BFS, 문제풀이 (0) | 2022.05.21 |
| [TIL] 05/18 항해99 10일차 - 해시 테이블, 문제풀이 (0) | 2022.05.19 |
| [TIL] 05/17 항해99 9일 차 - 큐(Queue), 문제풀이 (0) | 2022.05.18 |
| [TIL] 05/16 항해99 8일 차 - 스택(Stack), 문제풀이 (2) | 2022.05.16 |

들어가며
알고리즘 1주차가 끝나는 날이다. 항해99 알고리즘 주차에서는 한 주차가 끝날 때마다 테스트를 보게되고, 오늘 그 테스트를 보았다. 사실 1주차 내내 개념 정리에 주로 힘을 써왔기 때문에 구현에는 자신이 없어서 테스트를 잘 볼 수 있을까 걱정했는데 아니나 다를까 어렵더라… 어찌저찌해서 결국 해결은 했는데 문제를 풀어냈다!라는 기쁨보다는 여전히 한참 부족하다는 자괴감이 많이 들었다. 테스트 2시간이었는데 시간이 부족해서 추가시간까지 쓰고 나서야 겨우 해결을 하는 바람에 오늘 문제공부를 할 시간이 부족했다.
…라고 오늘 문제풀이를 못하는 이유를 늘어놨는데 결론은 오늘의 TIL은 항해99의 커리큘럼에 따라 그래프와 DFS의 간단한 개념을 정리해보고자한다!
그래프
그래프는 정점(vertex)와 간선(edge)으로 구성된 한정된 자료구조를 의미한다.
출처 - 위키백과
정점과 간선은 비전공자인 나에게 익숙한 들어본 단어는 아니다. 쉽게 말하자면 정점(vertex)는 각각의 노드(Node)를 말하고, 간선(edge)는 각 노드를 연결하고, 노드 간의 관계를 표시한 선이며, 그래프는 각 정점 간의 관계를 표현하는 조직도라고 볼 수 있다.


자료구조로서의 그래프는 수학자 오일러(Euler)에 의해 창안되어 오랜 기간 연구되어왔지만, 컴퓨터 과학 분야에서 그래프 알고리즘을 다루기 시작한 건 오래되지 않았다고 한다. 그래서 아직 더 쉽게 연구되지 않았고, 공부하는 사람들에게 고통을 안겨주고있다.
본격적인 그래프의 개념으로 들어가기 전에 오일러가 그래프를 창안하게 된 오일러 경로에 대해 간단하게만 알아보고 시작하자.

오일러 경로
우리가 종종 해봤던 한붓그리기가 바로 오일러 경로이다. 아주 옛날에 쾨니히스베르크에 흐르던 프레겔 강에는 2개의 큰 섬이 있었고 섬과 도시를 연결하는 7개의 다리가 놓여있었는데, 어느날 시민 한명이 “이 7개 다리를 한 번씩만 건너서 모두 지나갈 수 있을까?”라는 문제를 냈다고 한다.
모두가 쉽게 풀릴거라고 예상했던 것과 달리 이 문제를 풀 수 있는 이는 아무도 없었다.
이 문제를 연구하던 사람 중 한명이 바로 ‘수학의 모차르트'라고 불리는 레온하르트 오일러였다.
오일러는 이 문제가 도형 문제처럼 보이지만 당시까지 알려진 기하학으로는 풀수 없음을 알았고, 미지의 영역에 그 해법이 있다는 사실을 간파한 것이 ‘그래프 이론’의 시작이라고 한다.
오일러 경로 이외에도 해밀턴 경로, 외판원 문제등 그래프와 관련된 알고리즘 문제들이 존재하니 궁금하다면 구글에게 물어보는걸로 하고, 다시 그래프의 개념으로 넘어가보자.
그래프에서 사용하는 용어
어려운 개념이니 만큼 용어를 알지 못하면 두배로 어려워질테니 용어부터 알고 가자.
| 정점(vertice) | 노드(node)라고도 하며 정점에는 데이터가 저장된다. |
| 간선(edge) | 링크(link)라고도 하며 노드간의 관계를 나타냅니다. |
| 인접 정점(adjacent vertex) | 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점을 뜻한다. |
| 단순 경로(simple-path) | 경로 중 반복되는 정점이 없는것. 같은 간선을 자나가지 않는 경로. |
| 차수(degree) | 정점에 연결된 간선의 수를 말한다. |
| 진출 차수(out-degree) | 방향그래프에서 사용되는 용어로 한 노드에서 외부로 향하는 간선의 수를 뜻한다. |
| 진입차수(in-degree) | 방향그래프에서 사용되는 용어로 외부 노드에서 들어오는 간선의 수를 뜻한다. |
대표적인 그래프의 종류
무방향 그래프 (Undirected Graph)
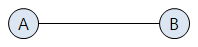
두 정점을 연결하는 간선에 방향이 없는 그래프. 양방향으로 이동이 가능하다.
방향 그래프 (Directed Graph)

두 정점을 연결하는 간선에 방향이 존재하는 그래프. 간선의 방향으로만 이동이 가능하다.
가중치 그래프 (Weighted Graph)
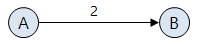
간선에 비용(cost) 또는 가중치(weight)가 할당된 그래프. 두 정점을 이동할 때 비용이 드는 그래프로, 네트워크(network)라고도 불린다.
완전 그래프 (Complete Graph)

모든 정점 간에 간선이 존재하는 그래프.
그래프의 구현 방법
그래프의 구현 방법에는 배열을 사용하는 인접 행렬(Adjacency Matrix)과 연결리스트를 사용하는 인접 리스트(Adjacency List)가 있다.
인접 행렬 (Adjacency Matrix)

인접 행렬은 2차원 배열로 그래프의 노드간 연결 관계를 표현한 것이다.
그림처럼 1 2 3 4 5 6 각각의 정점과 인접해있는 정점은 1, 인접하지 않은 정점은 0을 넣어준다. 참고로 자기 자신으로 연결되는 간선이 없으므로 배열의 대각선은 모두 0이다.
이를 배열로 표현하면 다음과 같다.
graph = [
[False, True, False, False],
[True, False, True, False],
[False, True, False, True],
[False, False, True, False]
]
장점
- 2차원 배열에 모든 저점들의 간선 정보가 있기 때문에, 두 정점을 연결하는 간선을 조회할 때
O(1)시간 복잡도로 가능하다. - 정점의 차수를 구할 때는 인접행렬의 i번째 행의 값을 모두 더하면 되므로
O(n)의 시간 복잡도로 가능하다. - 구현이 비교적 간단하다.
단점
- 간선의 개수와 무관하게 항상 n^2 크기의 2차원 배열이 필요하므로 메모리 공간이 낭비된다.
- 그래프의 모든 차수를 알아내려면 인접행렬 전체를 확인해야 하므로
O(n^2)의 시간이 소요된다.
인접 리스트 (Adjacency List)

인접 리스트는 각 정점에 인접한 정점들을 연결 리스트로 표현한 것이다. 그림은 무방향 그래프를 나타낸 것인데, 무방향 그래프의 경우에는 각 정점에 연결된 모든 정점을 저장한다.
이를 딕셔너리로 표현하면 다음과 같다.
graph = {
0: [1],
1: [0, 2]
2: [1, 3]
3: [2]
}
장점
- 정점들의 연결 정보를 탐색할 때
O(n)의 시간 복잡도로 가능하다. - 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.
단점
- 두 정점을 연결하는 간선을 조회하거나 정점의 차수를 알기 위해서는 정점의 인접 리스트를 탐색해야 하므로 인접 행렬에 비해 시간이 오래 걸린다.
- 구현이 비교적 어렵다.
인접 행렬 vs 인접 리스트
인접 행렬과 인접 리스트의 차이를 간단하게 정리하자면
인접 행렬은 시간이 빠르지만 공간이 낭비되고, 인접 리스트는 공간의 낭비가 적지만 시간이 비교적 느리다.
그래프 탐색 (순회)
깊이 우선 탐색 (DFS, Depth First Search)

DFS는 특정 노드에서 시작해 다음 분기로 넘어가기 전에 해당 분기를 완전히 탐색하는 방법이다.
쉽게 말하면, 갈 수 있는 만큼 최대한 깊이 가고 더 이상 갈 곳이 없다면 이전 정점으로 돌아가는 방식으로 그래프를 순회하는 방식이다.
DFS는 일반적으로 스택으로 구현하기는 하지만 재귀를 이용하면 조금 더 간단하게 구현할 수 있어서 코딩 테스트 시에 재귀 구현이 더 선호되는 편이라고 한다.
DFS를 예시를 들어가며 자세하게 설명해주는 글이 있어 첨부한다.
[알고리즘] 깊이 우선 탐색, DFS(Depth First Search)알고리즘이란?
DFS 구현하기
재귀 구조로 구현한 코드
DFS를 재귀를 이용하여 구현한 구체적인 동작 과정은 다음과 같다.
- 탐색 시작 노드를 스택에 삽입하고 방문처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접노드가 있으면 다시 함수를 재귀 호출한다
- 종료가 되면 방문한 노드를 순서대로 리턴한다.
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
def dfs_recursive(node, visited):
# 방문처리
visited.append(node)
# 인접 노드 방문
for adj in graph[node]:
if adj not in visited:
dfs_recursive(adj, visited)
return visited
assert dfs_recursive(1, []) == [1, 2, 5, 6, 7, 3, 4]
위 코드의 흐름을 그림으로 나타내면 다음과 같다.

재귀 구조는 포스팅을 쓸 때마다 느끼는 거지만 글로 설명하기가 되게 어렵다. 사실 글로 표현을 한다 하더라도 이해하기가 그닥 쉽지는 않다.
고민하던 차에 항해99 과제톡에서 다른 수강생분이 아주 유용한 웹사이트를 알려주셨기에 기록 겸 링크를 걸어두겠다.
https://pythontutor.com/visualize.html#mode=edit
Python Tutor - Visualize Python, Java, JavaScript, C, C++, Ruby code execution
Write code in Python 3.6 Java 8 JavaScript ES6 C (gcc 9.3, C17 + GNU extensions) C++ (g++ 9.3, C++20 + GNU extensions) ------ [unsupported] Python 2.7 [unsupported] C (gcc 4.8, C11) [unsupported] C++ (g++ 4.8, C++11) [unsupported] TypeScript 1.4 [unsupport
pythontutor.com
코드를 넣으면 그 코드를 그림으로 한줄한줄 표현해주는 사이트인데 코드의 흐름을 이해하기에 매우 도움이 된다.
재귀 구조의 경우 코드만 보고서는 이해하기가 힘들기 때문에 그림으로 보면 이해가 쏙쏙 되는데 이렇게 코드 한줄한줄을 직관적으로 보여주니 너무 좋다. 웹사이트 이름이 <파이썬 튜터>이지만 JAVA, JS, C, C++ 모두 선택 가능하니 사용해보는 걸 추천한다!
스택을 이용한 반복 구조로 구현한 코드
스택을 이용한 DFS의 구체적인 동작 과정은 다음과 같다
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
def dfs_stack(start):
visited = []
# 방문할 순서를 담아두는 용도
stack = [start]
# 방문할 노드가 남아있는 한 아래 로직을 반복한다.
while stack:
# 제일 최근에 삽입된 노드를 꺼내고 방문처리한다.
top = stack.pop()
visited.append(top)
# 인접 노드를 방문한다.
for adj in graph[top]:
if adj not in visited:
stack.append(adj)
return visited
assert dfs_stack(1) == [1, 4, 3, 5, 7, 6, 2]
마치며
과제를 풀지 못한 상태에서 과제톡을 들었는데, 설명을 들으면서 책을 봤을 때 코드가 이해하기가 어려웠다.
DFS가 되게 어려운 알고리즘이라고 많은 분들이 말하시는데 과제톡을 통해서 확실히 깨달았다. 앞으로 더 어려운 개념들이 나올텐데 많은 공부가 필요할 것 같다.
출처
https://suyeon96.tistory.com/32
https://coding-factory.tistory.com/610
'Study > TIL' 카테고리의 다른 글
| [TIL] 05/21 항해99 13일차 - 보안 공격, 백트래킹, 문제풀이 (0) | 2022.05.22 |
|---|---|
| [TIL] 05/20 항해99 12일차 - BFS, DFS vs BFS, 문제풀이 (0) | 2022.05.21 |
| [TIL] 05/18 항해99 10일차 - 해시 테이블, 문제풀이 (0) | 2022.05.19 |
| [TIL] 05/17 항해99 9일 차 - 큐(Queue), 문제풀이 (0) | 2022.05.18 |
| [TIL] 05/16 항해99 8일 차 - 스택(Stack), 문제풀이 (2) | 2022.05.16 |
